Khi tất cả các phân tích học máy đều đã lỗi thời: overfitting (không) tồn tại.

Bài đăng này đã không được cập nhật trong 4 năm

Lý thuyết: Cổ điển (không còn gì) chưa được phân tích.

Nếu các bạn được học kỹ hơn về học máy, thì chắc hẳn các bạn đã được nghe về các khái niệm sau đây:

Vapnik-Chervonenkis (VC) dimension: giá trị này cho biết khả năng phân lớp của tất cả các loại data có thể cho vào, về cơ bản là độ phức tạp của mô hình một cách thực tiễn.
Rademacher complexity: đo độ phức tạp của data đưa vào bằng cách so sánh nó với một phân bố nào đó.
Hoeffding's bound: sử dụng bất đẳng thức này để giới hạn độ chênh lệch giữa kết quả lúc training và kết quả ngoài đời thật (dưới một số giả thiết cơ bản)
Bias-Variance tradeoff: khi chọn model (hay nói chung là bất cứ quyết định gì), bạn đang đánh đổi giữa bias (bị ảnh hưởng bởi data) và variance (khả năng generalize của mô hình). Một mặt, nếu bias cao, thì mô hình sẽ cố khớp với training data, nhưng variance sẽ thấp, làm khả năng data được dự đoán đúng thấp -> underfit. Nếu variance cao, máy sẽ có khả năng cao, nhưng bias sẽ thấp, dự đoán sẽ fit hoàn hảo mặc kệ các tính chất của data -> overfit. Khái niệm này quan trọng nên cần một tấm hình minh họa: 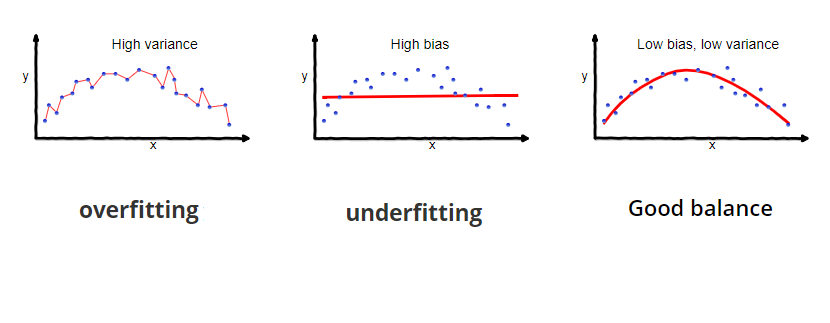Và ảnh minh họa của loss mô hình tách ra làm 2 phần trên:

Tất cả các kiến thức trên đều được nghiên cứu từ cơ bản dựa trên các kiến thức về ứng dụng xác suất thống kê và thuyết thông tin. Vậy tại sao các bạn bây giờ gần như chẳng ai biết về những cái này?

Thực tế: Thời đại này (không) phù hợp với các thuyết học máy cổ điển.

Tất cả lý thuyết trên đều đi xuống cống hết:

Với độ phức tạp của các mô hình hiện đại (ví dụ điển hình là các Transformers như BERT hhay GPT-2) với hàng trăm triệu các tham số, VC dimension của các mô hình đó cứ tạm gọi là to ơi là to.

_{Các mô hình trên paper/ngoài thực tế sau khi train đều được qua quá trình iterative pruning để giảm độ phức tạp và đồng thời bỏ những kết nối giữa các đặc tính không liên quan. Về iterative pruning, hãy đọc bài này của sếp Toàn team mình.}

Hoeffding's bound thường được sử dụng với các mô hình nhỏ; đồng thời được sử dụng vừa để có lý thuyết chống chân, vừa để có thể sử dụng hết tất cả data để train/validate mà không cần chia nhỏ để test. Tuy nhiên, đó là khi data còn khan hiếm; bây giờ data nhiều như nước sông Đà, và nếu nhưng làm cẩn thận tránh data snooping, thì kết quả trên test set là một ước lượng của loss trên tất cả các data ngoài thực tế, không bị ảnh hưởng bởi training data hay quá trình train (không cite được tại cơ bản quá, các bạn hãy đọc sách nếu cần tìm dẫn chứng).
Lý thuyết bảo không nên chọn mô hình quá phức tạp, nhưng thực tế các mô hình hiện tại đều vô cùng khổng lồ và chúng đều hoạt động! (sau khi đã sử dụng early stopping và regularization). Đáng lẽ ra test loss phải càng ngày càng tăng nếu model quá phức tạp, vì càng ngày càng overfit, nhưng thực tế lại không phải vây -- đây là hiện tượng được gọi là double descent, khi loss đi xuống 2 lần.

Phần chính: overfitting (không) tồn tại.

Nghe tuyệt quá phải không? Spoiler: nó chỉ đúng khi mô hình bạn đủ to thôi -- nhưng thời đại này cái gì chả to nhỉ.

Các thí nghiệm: Hiện thực (không như) dự tính.

Mô hình càng to càng dở? Sai!

Như đã nói ở trên, có hai quan điểm về lựa chọn kích cỡ mô hình ngược hoàn toàn với nhhau. Giả thiết được các nhà nghiên cứu đưa ra kết nối giữa kiến thức cổ điển và quan niệm học sâu hiện đại: có một điểm, tên là interpolation threshold, khi mô hình vừa đủ to để fit chính xác dataset (perfectly overfit). Trước điểm đó, các quan niệm cổ điển về cân bằng/đánh đổi bias-variance, với đường cong hình chữ V thần thánh. Sau điểm đó, mô hình sẽ thừa khả năng fit dataset, và đồng thời có thể nhận biết được các mối liên quan giữa các data/tính chất của input. Sau khi sử dụng early-stopping/regularization, mô hình sẽ không overfit và generalize tốt qua các data không có trong tập train.

Data càng nhiều càng tốt? Sai!

Lý do to nhất tại sao ngày nay là thời đại của deep learning, ngoài những sự phát triển vượt bậc của khả năng tính toán của máy tính, là sự đa dạng và số lượng vô kể của data. Một mô hình k có đủ data để train sẽ không thể có được kết quả tốt, nên mọi người từ lâu đã quan niệm là càng nhiều data càng tốt.

Sai!

... hoặc ít nhất là chỉ đúng một nửa. Tương tự việc chọn cấu hình mô hình, biểu đồ này cũng có một 2 điểm nhảy: càng nhiều data mô hình sẽ càng tốt (đúng như những gì đã được dự báo), tuy nhiên đến một điểm mà càng nhiều data thì mô hình lại càng ngày càng bội thực. Tuy nhiên điều may mắn là nếu cứ nhồi nó data nữa thì sẽ đến một lúc mô hình lại tốt lên lại. Vì vậy, có data thì cứ YOLO đi.

Train càng lâu càng dễ bị overfit? Quá sai! Sau khi bạn train đủ lâu, mô hình sẽ overfit như dự tính. Tuy nhiên , nếu bạn train tiếp, một cách nào đó loss sẽ thần kỳ lại hạ xuống và overfit sẽ biến mất? Khó hiểu.

Góc phân tích: Những lựa chọn (không) có lý do

Việc sử dụng mô hình teacher-student model trong trường hợp này là để chắc chắn data có thể được biểu diễn (nghĩa là không quá phức tạp). Cho dù, tất cả các phương trình đều có thể ước lượng bằng các mô hình tuyến tính (với các hàm kích hoạt phi tuyến tính); các ví dụ tiêu biểu nhất được viết ở đây.
Với một mô hình to, việc sử dụng early stopping hay regularization sẽ làm giảm độ phức tạp của mô hình một cách gián tiếp, phù hợp với lập luận của học máy xác suất cổ điển. Việc dừng sớm hay muộn phụ thuộc vào tính chất của nhiễu: nếu tỉ lệ giữa tín hiệu và nhiễu (SNR - signal-to-noise ratio) cao, model phải dừng học sớm, và ngược lại. Cụ thể hơn, nếu variance của nhiễu càng nhỏ so với variance của tham số cần tìm, điều đó cho thấy data càng có mối tương quan mật thiết, và mô hình càng phải dành thời gian ra để học các thông tin đó.
Hành vi của hàm mất mát với lượng tham số cao được Geiger and Spigler et. al nhận xét là khá giống với quá trình "jamming": khi lượng phần tử trong một hợp chất quá dày, chúng sẽ hóa thành thể rắn. Như bạn đã biết, trên thực tế tất cả vật chất đều tự đưa về trạng thái với độ ổn định cao nhất, khá là tương đương với quá trình tối ưu hóa của một mạng học máy. Tuy nhiên, thực sự mình chưa hiểu hết các lập luận của tác giả, nên nếu các bạn muốn, hãy đọc dẫn chứng số 2 trong danh sách link của bài này.

Ngoài ra thì hiện tại mới có các giả thiết/ý tưởng lý giải sơ bộ chứ chưa có nhiều chứng minh cụ thể lắm ¯\_(ツ)_/¯

Góc bình luận: Tôi (không phải) là Tạ Biên Cương.

Kết quả cho thấy các quyết định đều có xu hướng tương tự double descent, khi mô hình dở đi rồi lại tốt lên. Tuy nhiên, nghiên cứu này dừng khá sớm. Liệu hiện tượng này có phải là tuần hoàn? Có thể hiện tại chúng ta chưa đủ khả năng giải quyết/mò nghiệm bài toán này.
Việc train một mô hình sâu phụ thuộc rất nhiều vào điểm xuất phát ban đầu. Ví dụ, trong reinforcement learning chẳng hạn, một thí nghiệm bất kỳ có 70% khả năng thất bại. Vậy, liệu những kết quả trên đây có phải là do may mắn/xui xẻo?