Tìm hiểu về giải pháp Digital Humans phần 1: NeRF mô hình tái tạo các cảnh 3D bằng mạng nơ ron dựa trên trường bức xạ
1.Giới thiệu chung.
Nhiệm vụ tổng hợp hình ảnh người được điều khiển bởi âm thanh có rất nhiều ứng dụng, do đó, gần đây có nhiều nghiên cứu về chủ đề này. Nhiều phương pháp dựa trên việc sử dụng điểm đặc trưng (landmarks) và lưới (meshes) để làm thông tin cấu trúc khuôn mặt đã được phát triển, tức là sử dụng các đặc trưng trung gian làm cơ sở, và tất nhiên hiệu quả rất phụ thuộc vào các đặc trưng trung gian này.
Đặc biệt là khi NeRF (Neural Radiance Fields) xuất hiện lần đầu tại hội nghị ECCV năm 2020, chỉ sử dụng hình ảnh 2D làm tập huấn luyện và có thể tái tạo các cảnh 3D phức tạp của vật thể đó. NeRF có khả năng tái tạo các cảnh 3D vô cùng chân thực.
Từ đó nhiều phương pháp ra đời dựa trên NeRF để tổng hợp chân dung. NeRFace là phương pháp đầu tiên đưa 3DMM vào NeRF để kiểm soát phần đầu, còn một số phương pháp khác như sử dụng các đặc trưng âm thanh để điều khiển NeRF mà không sử dụng các đặc trưng trung gian. Tuy nhiên, nhược điểm của các phương pháp này là rất chậm, ví dụ như AD-NeRF cần 12 giây để tạo một khung hình 450x450 trên GPU 3090, rất xa so với yêu cầu 25FPS, và cần khoảng một ngày để huấn luyện một người, làm hạn chế việc sử dụng thực tế.
Hai nghiên cứu gần đây nhất là RAD-NeRF và ER-NeRF phát triển từ NeRF để tạo ra các biểu diễn con người nói chuyện được điều khiển bởi âm thanh với chất chất lượng cao và độ trễ thấp. Mục tiêu là cho phép người dùng trải nghiệm môi trường ảo chi tiết và sống động như thế giới thực, đồng thời cho phép người dùng khám phá và sửa đổi nó thông qua các tương tác đơn giản.
Demo những gì RAD-NeRF có thể làm được: https://me.kiui.moe/radnerf/
Demo ER-NeRF + text to speech:
2.Đầu tiên hãy tìm hiểu về NeRF
2.1 NeRF(Neural Radiance Fields)
NeRF, với danh nghĩa là một trong những ứng cử viên cho giải "Bài báo xuất sắc nhất" tại ECCV 2020, là một trong những bài báo kinh điển đáng để nghiên cứu kỹ lưỡng. Tuy nhiên, NeRF bao gồm nhiều kiến thức về đồ họa máy tính, khiến cho việc đọc và hiểu với những CVer thuần túy trở nên khá khó khăn 😂 . Bài viết này nhằm mục đích giải thích những nguyên lý cơ bản của NeRF bằng các khái niệm đơn giản, dễ hiểu. Nếu có điều gì không rõ, hãy để lại bình luận để thảo luận nhé.
NeRF, viết tắt của Neural Radiance Field. Để hiểu NeRF, trước hết cần biết NeRF làm gì, câu trả lời là: tổng hợp góc nhìn mới cho các cảnh 3D. NeRF là một kỹ thuật sử dụng mạng Neural để biểu đạt ngầm cảnh 3D.

NeRF thực hiện nhiệm vụ gì? NeRF nhận vào một loạt góc nhìn đã biết, tối ưu NeRF để biểu diễn cảnh liên tục, cuối cùng là tạo ra các góc nhìn mới của cảnh đó.
Giả sử chúng ta dùng NeRF để học một cảnh cụ thể, thì cảnh này được lưu trữ ngầm trong các tham số của mạng NeRF. Nếu cần có một góc nhìn mới, chúng ta cần dùng mạng NeRF đó để tính toán các giá trị ánh sáng và màu sắc tại mỗi vị trí của góc nhìn đó.
Để hiểu dễ dàng hơn, hãy xem xét ví dụ bằng hình ảnh 2D:
Chúng ta có một bức ảnh 2D, tọa độ của các điểm ảnh là (x, y), màu của các điểm ảnh là c. Vì các tọa độ và màu sắc có sự liên hệ rõ ràng, liệu chúng ta có thể tạo ra một mối quan hệ ánh xạ không?
Thử một VD nha. Giả sử ta có một hình 2x2:

Ta cần tìm một hàm f(x,y) sao cho thỏa mãn:
- f(1,1)=0
- f(1,2)=1
- f(2,1)=0
- f(2,2)=0
0 ứng với màu trắng và 1 ứng với màu đen.
Dễ thấy: hàm . Như vậy, 1 hàm f(x,y) hoàn toàn có thể dự đoán màu của 1 ảnh từ tọa độ (x,y) từ trước.
Quan hệ ánh xạ này có thể được biểu diễn bằng mạng neural không? Hoàn toàn có thể, hàm f(x) như thế này có thể biểu diễn xấp xỉ bằng một mạng nơ ron:
Chúng ta có thể lấy mẫu một số điểm ngẫu nhiên từ hình ảnh để làm dữ liệu huấn luyện cho mạng neural, sau đó dùng mạng neural được huấn luyện để suy ra các giá trị điểm ảnh ở các vị trí khác trên bức ảnh. Từ đây, ta có thể dễ dàng hiểu được ý tưởng cơ bản của NeRF bằng cách mở rộng từ 2D sang 3D. Công thức của NeRF là:
Trong công thức (3),
- là tọa độ của điểm 3D,
- là hướng quan sát,
- là giá trị màu được dự đoán của điểm 3D,
- và là mật độ vật thể (sẽ được giải thích sau).
Khi so sánh công thức (1) và (3), ta thấy có một số khác biệt, chẳng hạn như khi mở rộng từ mặt phẳng sang 3D, nhiều yếu tố cần được xem xét, trong đó góc quan sát sẽ ảnh hưởng đến cách điểm 3D thể hiện màu sắc. Do đó, thiết kế của NeRF dựa trên quan điểm phụ thuộc vào góc nhìn (view-dependent), nên đầu vào của NeRF ngoài vị trí 3D còn cần góc quan sát, tổng cộng là 5 chiều, tức là . Kết quả đầu ra là giá trị màu của điểm 3D và mật độ vật thể . Hai đầu ra này sẽ được sử dụng cho việc thể hiện đồ họa theo phương pháp "kết xuất thể tích" (volume rendering).
2.2 Huấn luyện NeRF
Để hiểu NeRF, trước tiên cần nắm một vài khái niệm. Một, camera ray là gì? Câu trả lời là: tia từ máy ảnh.
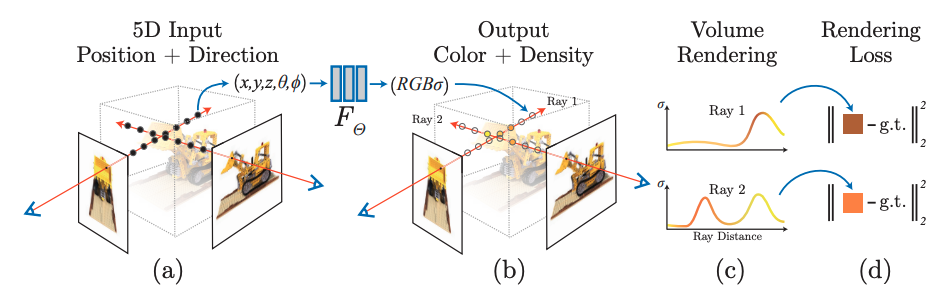
Từ Hình trên, chúng ta thấy rằng NeRF có đầu vào 5 chiều và đầu ra 4 chiều . Vậy hai tham số đầu vào biểu thị hướng quan sát, và , có ý nghĩa gì? Mọi người có thể theo dõi ví dụ sau:
Cố định , thay đổi :

Cố định , thay đổi :

Qua hai ảnh động trên, chúng ta có thể hiểu rằng θ và ϕ kiểm soát các góc độ khác nhau - sơ lược có thể hiểu ϕ là góc độ "gật đầu", còn θ là góc độ "lắc đầu".
Như trong hình (a2) , với một góc nhìn đã biết, chúng ta có thể tạo ra một tia từ mỗi điểm 2D, sau đó thực hiện lấy mẫu nhiều điểm dọc theo hướng của tia (tức là theo chiều sâu). Nếu chưa rõ về nguyên lý của tia, hãy tìm hiểu về mối quan hệ giữa tọa độ 2D của máy ảnh và tọa độ 3D. Dưới đây là một ảnh động minh họa:
Với biểu diễn hình ảnh 2D được miêu tả trong công thức (1), chúng ta chỉ cần biết tọa độ của điểm ảnh để xác định giá trị màu tương ứng. Nhưng đối với biểu diễn cảnh 3D, hình ảnh 2D được quan sát từ một điểm nhìn nhất định là kết quả của sự tổng hợp có trọng số của nhiều ảnh, mà những ảnh này được lấy mẫu từ các điểm dọc theo hướng của tia quan sát. Chính xác hơn, mỗi giá trị màu của điểm ảnh 2D là sự kết hợp có trọng số của các điểm lấy mẫu dọc theo tia 3D.
Hiểu đến đây, ta có thể quay lại Hình (2), trước tiên là xem hình (a), các điểm tròn đen là các điểm lấy mẫu dọc theo tia, mỗi điểm nhỏ này tạo ra một mẫu huấn luyện 9 chiều và có thể sử dụng để huấn luyện MLP. Trong giai đoạn suy luận, chúng ta cũng cần lấy mẫu trên tia quan sát. Do đó, NeRF sử dụng MLP để biểu diễn ngầm một cảnh. Nếu muốn có một góc nhìn mới, chúng ta cần lấy các giá trị của tất cả các điểm lấy mẫu dọc theo tia quan sát trong góc nhìn đó. Nếu độ phân giải của ảnh là 224x224 và mỗi tia lấy mẫu 16 điểm, thì MLP trong NeRF cần thực hiện 224x224x16 lần suy luận. Kết quả này có thể sử dụng để thực hiện rendering theo phương pháp thể tích (volume rendering). Hiểu phần này đồng nghĩa với việc đã nắm được nguyên lý cơ bản của NeRF.

Phân tích tiếp hình (b) và hình (c), Kết quả là các màu RBG và mật độ tại các điểm lấy mẫu được tính toán từ hàm ta có được 2 đồ thị của 2 tia (Ray 1 và Ray 2) như hình (c) . Nhận xét chủ quan 1 chút, Ray 1 có giá trị mật độ cao về gần cuối, có thể đó là do điểm lấy mẫu đang nằm trong mô hình cụ thể là ở phần chiếc gầu múc. Ray 2 có mật độ cao ở 2 bên trái và phải, nhưng lõm ở giữa khả năng là do điểm lấy mẫu ở giữa đang nằm ở khoảng không gian trống (khe nhỏ bên trong gầu múc của mô hình).
Tới Hình (d) các giá trị màu và mật độ sau khi được tổng hợp sẽ được tính ra màu cụ thể và so sánh với màu của pixel gốc để tính toán lỗi. Và với số lượng ảnh đủ lớn, kèm với nhiều góc độ. Việc một mạng neural có thể học được các giá trị màu của từng điểm lấy mẫu là hoàn toàn có thể từ đó tổng hợp lên được vật thể 3 chiều.
Quá trình lan truyền tiến:
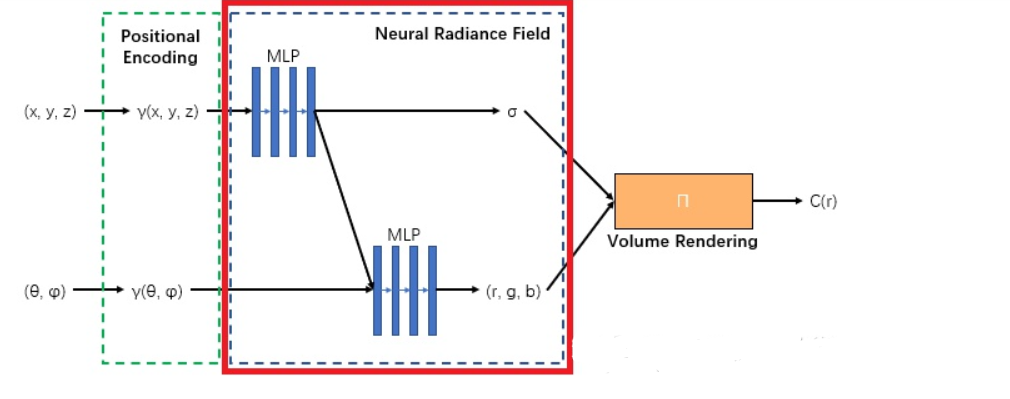
Vị trí sau khi được mã hóa sẽ được đưa vào một mạng MLP để tính ra mật độ , và lấy đầu ra đó kết hợp với hướng để tính toán ra màu theo hướng tại từng điểm, tổng hợp các điểm theo tia ta được màu . Sau đó so sánh màu với ta sẽ tính được loss của mô hình. Rồi cập nhật lại trọng số.
Ngoài ý tưởng này, trong paper có nhắc đến một số thủ thuật mà họ sử dụng để tăng độ chính xác và chân thật hơn cho mô hình 3D. Đầu tiên là mã hóa vị trí.
2.3 Mã hóa vị trí
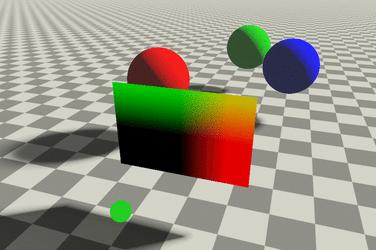
Trong NeRF, mã hóa vị trí nhằm tránh vấn đề làm mịn quá mức các điểm lấy mẫu liền kề về mặt không gian trong biểu diễn MLP . Ví dụ: nếu hai điểm vị trí (237, 332, 198) và vị trí (237, 332, 199) được sử dụng làm đầu vào của MLP, MLP có thể không đủ nhạy với chữ số hàng đơn vị, dẫn đến vấn đề vượt quá làm mịn đầu ra. Ví dụ:

do thiếu mã hóa vị trí nên chi tiết ở những vùng có họa tiết tương tự nhau sẽ bị mất.
Công thức Mã Hóa Vị Trí trong paper:
VD:
Một nhận xét chủ quan 😅. Ngoài việc biểu diễn tốt hơn được những thay đổi giữa các vị trí gần nhau, việc thêm mã hóa vị trí như thế này cũng giúp mô hình tăng số chiều của input. Để ý ví dụ 2D ban đầu, nếu số chiều tọa độ đầu vào không đủ lớn mà số lượng phương trình cần giải quá nhiều thì hàm f(x) sẽ rất phức tạp thậm chí vô nghiệm. Việc cố gắng tìm 1 hàm f(x) thoải mãn quá nhiều phương trình thực sự rất phức tạp phải không nào 😗
Nhưng số chiều của input nhiều quá cũng không tốt, nếu không sẽ xảy ra hiện tượng Curse, Curse chỉ ra rằng, trong không gian chiều cao, dữ liệu trở nên thưa thớt, điều này làm cho việc sử dụng phương pháp thống kê hoặc học máy trở nên rất khó khăn.
Trong paper thì với và với . Tức là đầu vào của (x,y,z) tăng từ 3 chiều lên chiều.
2.4 Lấy mẫu phân cấp
Chiến lược lấy mẫu ban đầu không hiệu quả vì mỗi điểm lấy mẫu được xử lý như nhau. Nhưng các vùng trống và vùng bị che khuất không ảnh hưởng đến hình ảnh được hiển thị mà vẫn được lấy nhiều. Tác giả áp dụng cách biểu diễn phân cấp để cải thiện hiệu quả hiển thị. Phương pháp cụ thể là: sử dụng hai mạng để thể hiện một cảnh (một dày, một mỏng). Trước tiên, hãy sử dụng lấy mẫu thông thường để đánh giá mạng "thô", sau đó sử dụng mạng "thô" để đánh giá và chọn ra nhiều mẫu có nhiều thông tin hơn, chẳng hạn như điểm lấy mẫu nào hữu ích hơn cho việc hiển thị khối.
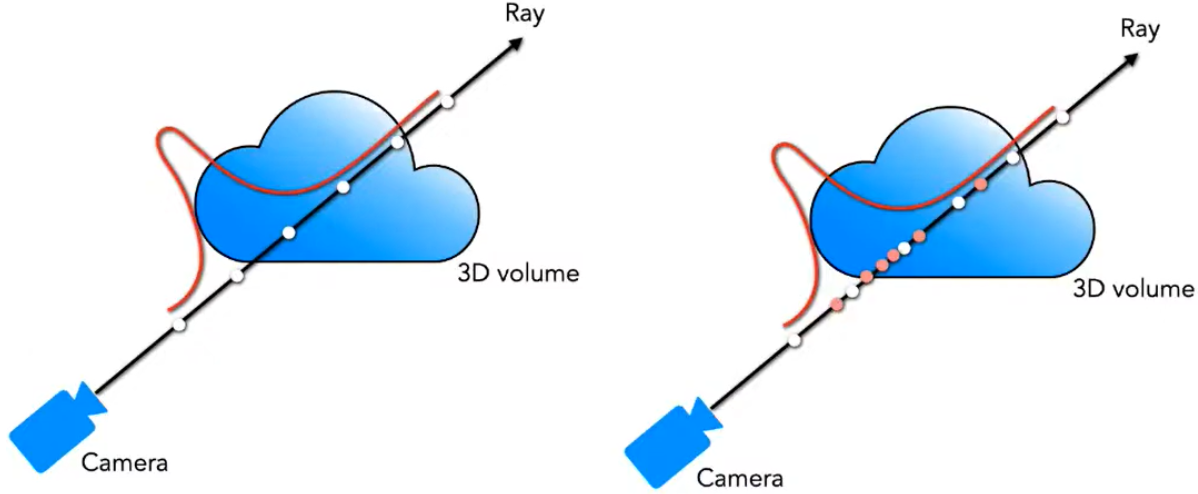
Bằng cách tạo ra hàm mật độ xác suất dọc theo hướng tia, như thể hiện trong hình bên trái. Thông qua hàm mật độ xác suất này, chúng ta có thể thu được một cách đại khái sự phân bố của các vật thể theo hướng tia. Từ đó có thể lấy được nhiều điểm lấy mẫu hơn từ những khu vực chứa nhiều nội dung hiển thị hơn.
Chính vì cách này, hàm tính toán lỗi cũng sẽ tính toán lỗi của cả 2 tập các điểm lấy mẫu thô và lấy mẫu mịn:
- là tập hợp các tia sáng (rays) trong mỗi lô dữ liệu (batch).
- là màu thực tế (ground truth),
- là màu dự đoán từ mô hình thô (coarse),
- là màu dự đoán từ mô hình mịn (fine).
2.5 Volume Rendering
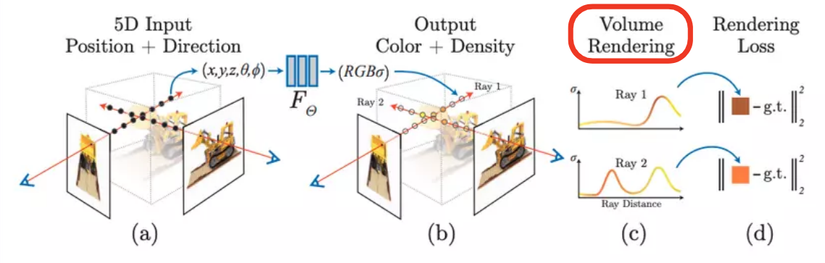
Khó khăn cuối cùng để hiểu NeRF là Volume Rendering. Trong quá trình đào tạo NeRF ở trên, chúng ta đã biết rằng NeRF sẽ dự đoán từng điểm lấy mẫu trong mỗi tia và để tính giá trị RGB của từng pixel trong ảnh mới, yêu cầu giá trị của tất cả các điểm lấy mẫu trên tia này để quyết định. Tác giả thực hiện điều này bằng cách sử dụng mô hình vật lý về sự hấp thụ ánh sáng để thể hiện nó.
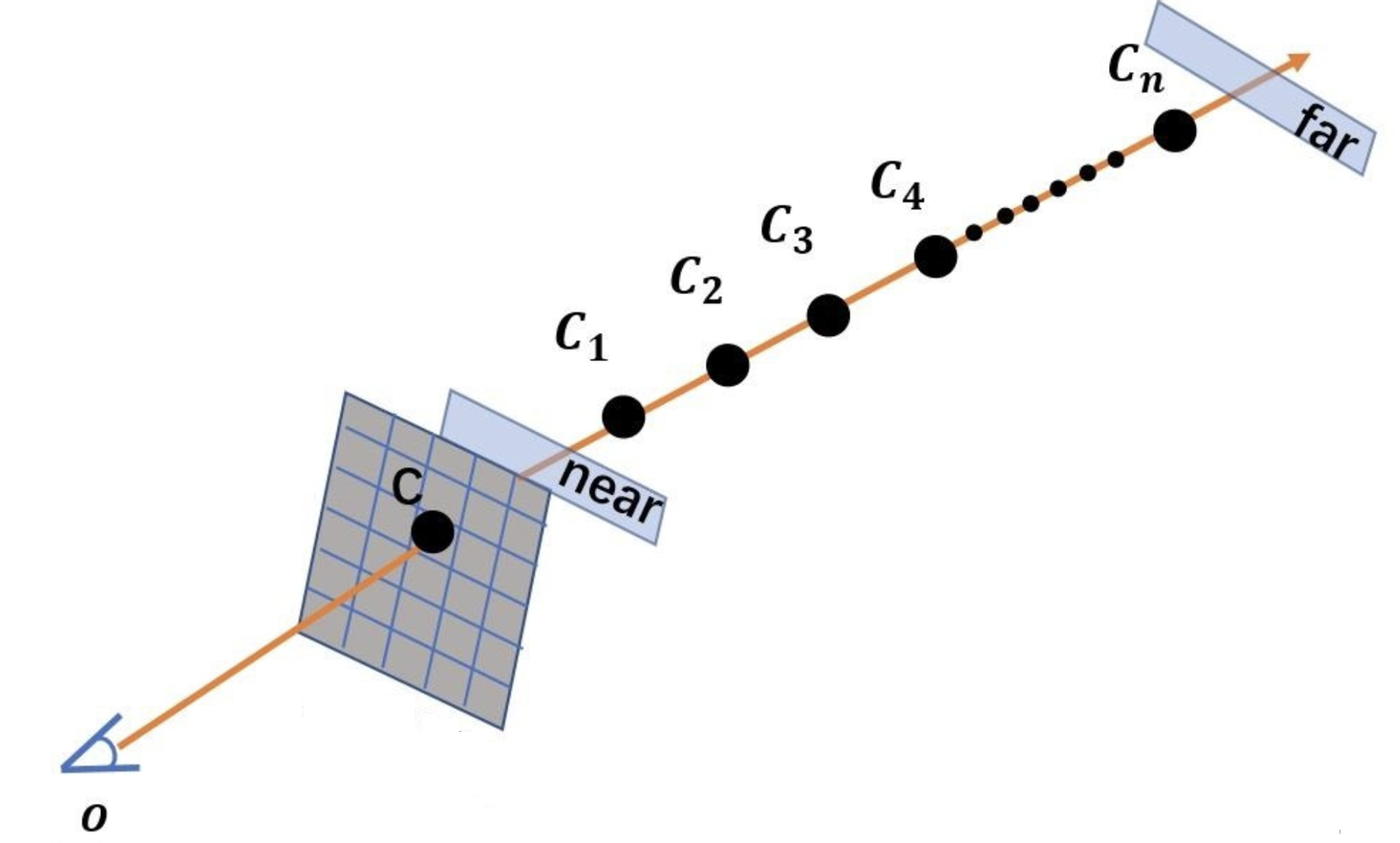
Công thức trên được sử dụng trong lý thuyết nhưng trong thực tế, các điểm lấy mẫu không liên tục nên để tính toán màu ta sử dụng tổng của các điểm lấy mẫu rời rạc để tính toán, các công thức sau để tính toán:
trong đó
Khi xét một góc nhìn mới, giá trị màu của từng pixel được xác định bởi một tia. Điểm bắt đầu của tia này là tâm quang học. Khi tâm quang học trỏ đến một pixel cụ thể trong mặt phẳng hai chiều của ảnh, tia này có thể xác định giá trị màu của pixel này. xác định khoảng cách giữa điểm với tâm quang học. Thông thường, chúng ta chỉ lấy mẫu tia và đầu ra MLP của các điểm lấy mẫu thưa thớt sẽ xác định giá trị màu của pixel này. Sau khi hiểu đoạn này, chúng ta hãy xem các thành phần của công thức:
- định nghĩa xác suất mà tia không chạm vào bất cứ vật thể gì tính từ tâm quang học tới điểm lấy mẫu. mũ 0 sẽ là 1. Khi tia đi xuyên qua càng nhiều vật chất thì đại lượng này sẽ càng nhỏ.
- : mật độ thể tích có thể xác định "tầm quan trọng" của điểm lấy mẫu. Điểm lấy mẫu gần tâm quang học hơn có trọng số cao hơn .
- giá trị màu tại điểm lấy mẫu theo hướng d.
Do khả năng thể hiện ngầm thông tin ba chiều vượt trội nên sau đó NERF đã phát triển nhanh chóng theo hướng tái thiết ba chiều, và một trong những ứng dụng đó là để tái tạo và điều khiển phần đầu con người.
Các ứng dụng của NeRF:

Để nâng cao hiệu quả, một số giải pháp cải tiến hiệu quả NeRF đã được phát triển như đã được giới thiệu. Mục tiêu là giảm kích thước MLP trong khi vẫn bảo toàn các tính năng của cảnh 3D trong cấu trúc lưới. MLP tiêu tốn nhiều tài nguyên trước đây đã được thay thế bằng phép nội suy tuyến tính, phương pháp này cũng có thể lấy thông tin của từng điểm vị trí 3D, nhưng phương pháp tổng hợp cảnh tĩnh này không được sử dụng để trực tiếp tổng hợp cho cảnh động để phục vụ cho tổng hợp digital human.
Để tiếp tục, hãy tìm hiểu về RAD-NeRF ở phần 2.
Nếu có thắc mắc gì xin vui lòng để lại bình luận nhé 😆
Nguồn tham khảo: https://arxiv.org/abs/2211.12368
All rights reserved
