Rotary Position Embedding - RoPE: Sợi dây thắt chặt mối liên hệ về mặt vị trí trong mô hình Transformer
Trong những năm gần đây, các mô hình Transformer đã trở thành xương sống của hầu hết các tiến bộ trong lĩnh vực xử lý ngôn ngữ tự nhiên (NLP) và thị giác máy tính (CV). Tuy nhiên, bản chất không tuần tự của Transformer lại khiến việc mã hóa thông tin về thứ tự và vị trí trở thành một thách thức lớn. Để giải quyết vấn đề này, các kỹ thuật Position Embedding (mã hóa vị trí) đã được phát triển, từ phương pháp mã hóa tuyệt đối (Absolute Position Encoding) đến mã hóa tương đối (Relative Position Encoding).
Dù vậy, các phương pháp truyền thống vẫn gặp một số hạn chế, chẳng hạn như thiếu tính liên tục hoặc khả năng mã hóa mối quan hệ tương đối giữa các token một cách mượt mà. Đây chính là lúc Rotary Position Embedding (RoPE) xuất hiện như một giải pháp đột phá, không chỉ bảo toàn thông tin vị trí mà còn duy trì sự mượt mà và ổn định trong không gian mã hóa.
1. Ôn lại bài cũ
1.1. Position Embedding
Trong các mô hình Transformer, một thách thức cơ bản là làm sao để mã hóa thông tin về thứ tự của các token trong chuỗi dữ liệu. Vì Transformer không xử lý dữ liệu theo tuần tự (như RNN), nên nó không có khái niệm "vị trí" tự nhiên. Điều này dẫn đến nhu cầu tích hợp thông tin vị trí trực tiếp vào các đầu vào của mô hình, và Position Embedding (mã hóa vị trí) ra đời để giải quyết vấn đề này.
Position Embedding là một kỹ thuật thêm thông tin vị trí vào vector biểu diễn của mỗi token trong chuỗi, giúp mô hình Transformer có khả năng phân biệt vị trí của các token. Kỹ thuật này có hai cách tiếp cận phổ biến:
-
Absolute Position Encoding (Mã hóa vị trí tuyệt đối):
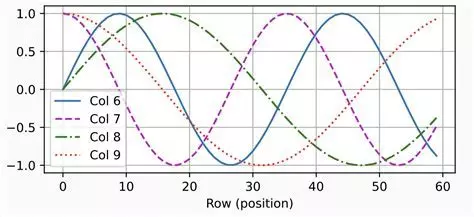
- Với phương pháp này, mỗi vị trí trong chuỗi được gán một vector biểu diễn riêng biệt, thường dựa trên các hàm sin và cos với tần số khác nhau.
- Ưu điểm: Dễ hiểu và dễ triển khai.
- Nhược điểm: Không nắm bắt được mối quan hệ tương đối giữa các token và khó tổng quát hóa với các chuỗi dài hơn chuỗi huấn luyện.
-
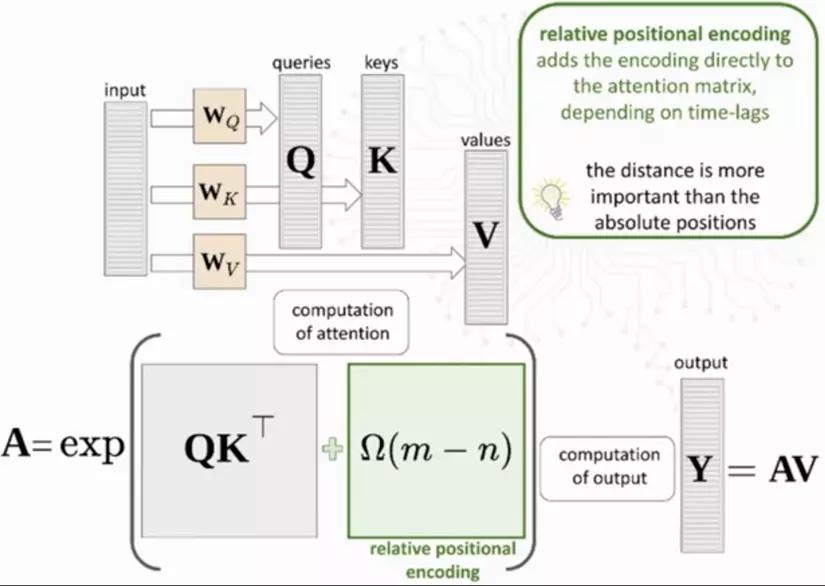
Relative Position Encoding (Mã hóa vị trí tương đối):
- Phương pháp này tập trung vào việc mã hóa khoảng cách tương đối giữa các token thay vì vị trí tuyệt đối của chúng. Điều này cho phép mô hình hiểu rõ mối quan hệ giữa các token bất kể độ dài chuỗi.
- Ưu điểm: Hiệu quả hơn trong việc nắm bắt ngữ cảnh và tổng quát hóa.
- Nhược điểm: Phức tạp hơn về mặt tính toán và triển khai.
Dù có nhiều cải tiến, cả hai phương pháp trên vẫn còn một số hạn chế như thiếu tính liên tục hoặc không thể bảo toàn cấu trúc mối quan hệ vị trí trong không gian cao.
1.2. Số phức
Số phức là một khái niệm trong toán học được mở rộng từ tập số thực, thường được sử dụng để biểu diễn các đại lượng có cả phần thực và phần ảo. Một số phức biểu diễn dưới dạng:
z = a + bi
Trong đó:
- a: Phần thực
- b: Phần ảo
- i: Đơn vị ảo
Phần kiến thức trên là phần chúng ta được học vào lớp 12. Nhưng phần này chúng ta đi thêm một chút phần kiến thức khác của số phức. Một đặc điểm nổi bật của số phức là khả năng biểu diễn dưới dạng cực. Dạng biểu diễn được biểu thị ở Image 3.

Một số tính chất đáng chú ý khi biểu diễn số phức ở dạng này.
Phép nhân hai số phức ở dạng cực

Phép chia hai số phức ở dạng cực
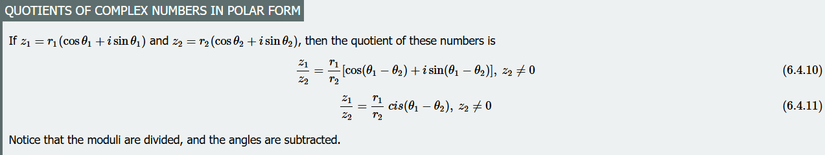
Phép xoay Khi nhân một số phức với , số phức đó sẽ được quay một góc ϕ trên mặt phẳng phức, trong khi vẫn giữ nguyên độ lớn.
Ngoài những khái niệm trên thì chúng ta sẽ làm quen thêm một khái niệm không kém quan trọng là không gian phức (Complex Plane): Số phức không chỉ là một khái niệm trừu tượng mà còn có ứng dụng thực tế trong việc biểu diễn vector trên mặt phẳng phức (complex plane):
- Vector không đổi độ lớn: Khi quay hoặc thực hiện phép biến đổi, độ lớn r của số phức không đổi, giúp bảo toàn thông tin quan trọng.
- Tính liên tục và mượt mà: Các biến đổi trên mặt phẳng phức diễn ra một cách liên tục, không có sự đứt gãy hay gián đoạn, tạo điều kiện thuận lợi cho các ứng dụng trong học sâu.
- Sự độc nhất trong việc biểu diễn: Trong không gian số phức thì mỗi số phức sẽ được biểu diễn dưới dạng cực duy nhất, đảm bảo tính chính xác và không bị nhầm lẫn khi biểu diễn.
2. Đi vào bài toán
Như chúng ta đã biết thì trong Transformer, layer Position Encoding sẽ là một lớp riêng biệt và những thông tin về vị trí sẽ được bổ sung vào với các từ. Điều này đem đến một số vấn đề:
- Không nắm bắt được vị trí tương đối giữa các token: Absolute positional encoding chỉ mã hóa thông tin vị trí tuyệt đối của từng token trong chuỗi, nhưng không thể biểu diễn mối quan hệ tương đối giữa các token, chẳng hạn như khoảng cách giữa hai từ trong ngữ cảnh.
- Khó khái quát hóa vượt quá độ dài tối đa: Absolute positional encoding thường được thiết kế với một chiều dài tối đa cố định. Khi mô hình phải xử lý các chuỗi dài hơn mức này, positional encoding không thể được mở rộng một cách tự nhiên, dẫn đến hiệu suất suy giảm.
- Embedding vị trí dạng hình sin có khả năng ngoại suy rất yếu: Các vị trí được mã hóa bằng hàm sóng hình sin và cosin có hiệu quả trong phạm vi giới hạn, nhưng khi xử lý các chuỗi nằm ngoài phạm vi được học, chúng không thể duy trì mối liên hệ vị trí một cách chính xác.
- Thiếu cách diễn giải hình học rõ ràng, khó để mô hình suy luận: Absolute positional encoding không có cách biểu diễn trực quan dựa trên hình học, điều này làm tăng độ phức tạp khi mô hình phải suy luận dựa trên thông tin vị trí. Điều này khiến mô hình khó xử lý những nhiệm vụ đòi hỏi tính toán về quan hệ vị trí giữa các token.
Ý tưởng chính của RoPE là sử dụng complex plane để biểu diễn thông tin về vị trí và nhúng trực tiếp thông về vị trí tương đối giữa các token vào trong quá trình truyền đạt thông tin giữa các từ, không cộng trực tiếp thông tin vị trí tuyệt đối ở ngoài như kiến trúc Transformer.
2.1. Công thức tổng quát
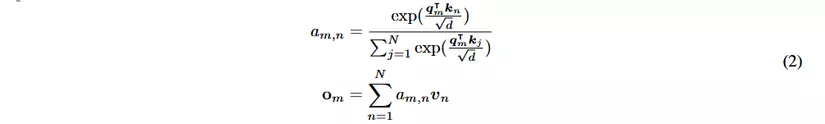
Dựa vào công thức trên thì chúng ta có thể thấy được rằng thường cho phép truyền đạt kiến thức giữa các token ở các vị trí khác nhau. Để tích hợp thông tin vị trí tương đối, chúng ta cần biểu diễn tích trong query và key dưới dạng một hàm , trong đó hàm này chỉ phụ thuộc vào các vector nhúng từ , và vị trí tương đối của chúng .
Lúc này chúng ta có tổng quan công thức như sau:
Và mục tiêu của chúng ta sẽ là tìm ra một cơ chế Mmã hóa tương đương để giải các hàm và nhằm tuân theo mối quan hệ đã đề cập ở trên.
2.2. Rotary position embedding
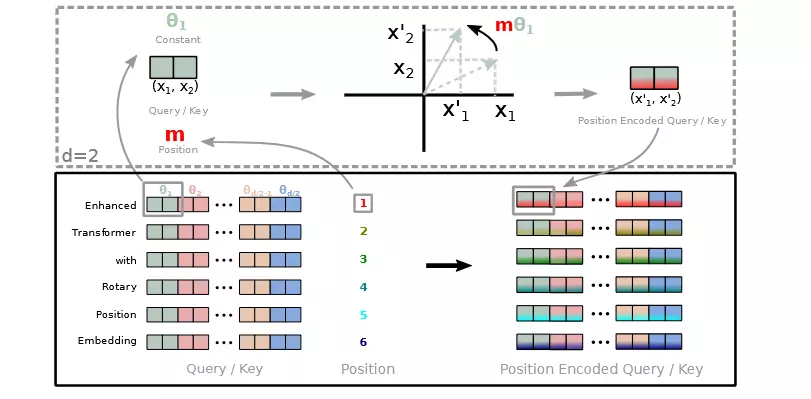
2.2.1. A 2D Case
Chúng ta sẽ bắt đầu với trường hợp có thể trực quan hóa. Khi này ta sẽ có công thức tổng quát hơn.
Trong đó:
- : Phần thực trong số phức
- biểu thị số phức liên hợp của
Mở rộng hơn thì chúng ta có công thức này.
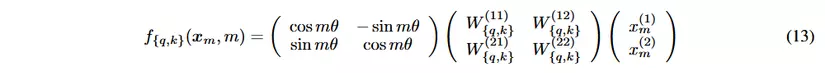
2.2.2. General form
Còn đối với dạng General Form thì nó sẽ coi chia thành d/2 subspaces và xử lý biến đổi tương tự.
Công thức tổng quát:

2.2.3. Các đặc tính của RoPE
RoPE có một số đặc tính sau:
- Long-term Decay
- Kết hợp với Linear Attention
Conclusion
RoPE đem lại nhiều giá trị về cách xử lý Positions Embedding, như việc đưa mối liên hệ về vị trí giữa các token trực quan và dễ thấy hơn. Phía trên là nhưng kiến thức cơ bản nhất về RoPE, còn mệnh đề chứng minh hay diễn giải các tầng toán học sâu hơn thì mình cx chưa đi quá sâu, mọi người có thể đọc thêm ở paper gốc hoặc một số bài viết mình có đính ở bên dưới. Cảm ơn vì đã dành thời gian đọc.
References
All rights reserved
