Phân tích dữ liệu chuỗi thời gian với Python
Trong kỷ nguyên số hiện nay, dữ liệu không chỉ đóng vai trò là tài sản quý giá mà còn là nguồn lực vô tận giúp các doanh nghiệp và tổ chức đưa ra những quyết định chiến lược. Một trong những loại dữ liệu quan trọng và phổ biến nhất là dữ liệu chuỗi thời gian. Dữ liệu chuỗi thời gian là dữ liệu được thu thập theo thời gian, thường được sử dụng để theo dõi các biến động theo thời gian của một hiện tượng hay quá trình nào đó. Từ kinh tế học, tài chính đến khoa học và kỹ thuật, dữ liệu chuỗi thời gian hiện diện trong hầu hết mọi lĩnh vực.
Trong hướng dẫn này, chúng ta sẽ cùng nhau khám phá thế giới phân tích dữ liệu chuỗi thời gian bằng Python. Từ những khái niệm cơ bản nhất đến các kỹ thuật phức tạp hơn, chúng ta sẽ đi sâu vào từng bước của quy trình phân tích và dự báo. Bằng cách nắm vững các phương pháp và công cụ cần thiết, bạn sẽ có khả năng biến những dữ liệu thô thành những thông tin quý giá, phục vụ cho việc ra quyết định và hoạch định chiến lược hiệu quả.
Trong bài viết này, chúng ta sẽ đi qua:
- Định nghĩa về dữ liệu chuỗi thời gian (time series) và đặc điểm của loại dữ liệu này
- Phương pháp để tiền xử lý and làm sạch dữ liệu (preprocess and clean data) để chuẩn bị cho bước phân tích
- Các kĩ thuật thường sử dụng để khám phá và trực quan hóa dữ liệu (explore and visualize data)
- Một vài phương pháp để phân tác dữ liệu
- Sau khi có dữ liệu,chúng ta sẽ tìm hiểu về một số phương pháp học máy để xây dựng mô hình dự đoán
- Đánh giá và lựa chọn model
Định nghĩa dữ liệu “time series”
Trong phần này, chúng ta sẽ tìm hiểu về dữ liệu “chuỗi thời gian” là gì và đặc điểm của loại dữ liệu này.
Định nghĩa
Dữ liệu chuỗi thời gian là một chuỗi các điểm dữ liệu được thu thập hoặc ghi lại tại các khoảng thời gian cụ thể. Ví dụ bao gồm giá cổ phiếu hàng ngày, số liệu bán hàng hàng tháng, dữ liệu khí hậu hàng năm và nhiều hơn nữa. Đặc điểm chính của dữ liệu chuỗi thời gian là trật tự thời gian của nó, nghĩa là thứ tự mà các điểm dữ liệu được ghi lại là quan trọng.
Các Đặc Điểm Dữ Liệu Chuỗi Thời Gian
Dữ liệu chuỗi thời gian có một số đặc điểm phân biệt nó với các loại dữ liệu khác:
- Xu hướng (Trend): Đây là sự di chuyển hoặc hướng đi dài hạn trong dữ liệu. Ví dụ, sự gia tăng chung trong doanh số bán hàng của một công ty qua nhiều năm.
- Tính thời vụ (Seasonality): Đây là các mô hình lặp lại theo khoảng thời gian cố định, chẳng hạn như doanh số bán kem tăng cao hơn vào mùa hè.
- Mô hình chu kỳ (Cyclic Patterns): Khác với tính thời vụ, các mô hình chu kỳ không có chu kỳ cố định. Chúng có thể bị ảnh hưởng bởi các chu kỳ kinh tế hoặc các yếu tố khác.
- Thành phần bất thường (Irregular Components): Đây là các biến đổi ngẫu nhiên hoặc không thể dự đoán trong dữ liệu.
Các loại dữ liệu chuỗi thời gian
Dữ liệu chuỗi thời gian đơn biến và đa biến:
- Đơn biến (Univariate): Một biến số hoặc đặc trưng duy nhất được ghi lại theo thời gian (ví dụ: nhiệt độ hàng ngày).
- Đa biến (Multivariate): Nhiều biến số được ghi lại theo thời gian (ví dụ: nhiệt độ hàng ngày, độ ẩm và tốc độ gió).
Chuỗi thời gian đều đặn và không đều đặn:
- Đều đặn (Regular): Các điểm dữ liệu được ghi lại ở các khoảng thời gian nhất quán (ví dụ: hàng giờ, hàng ngày).
- Không đều đặn (Irregular): Các điểm dữ liệu được ghi lại ở các khoảng thời gian không nhất quán.
Code python
import pandas as pd
import numpy as np
# Creating a sample time series data
date_range = pd.date_range(start='1/1/2020', periods=100, freq='D')
data = np.random.randn(100)
time_series = pd.Series(data, index=date_range)
print(time_series.head())
Đoạn code trên minh họa dữ liệu đơn biến với dữ liệu 100 ngày kể từ 1/1/2020
Tiền xử lý dữ liệu
Trước khi đi vào phân tích dữ liệu, một bước quan trọng chúng ta cần phải thực hiện đó là tiền xử lý dữ liệu đó để đảm bảo dữ liệu được chính xác và dáng tin cậy. Phần này sẽ xử lý các vấn đề mà tập dữ liệu thường gặp phải: thiếu dữ liệu (missing values), dữ liệu ngoại lệ (outlier), và biến đổi dữ liệu (transform data)
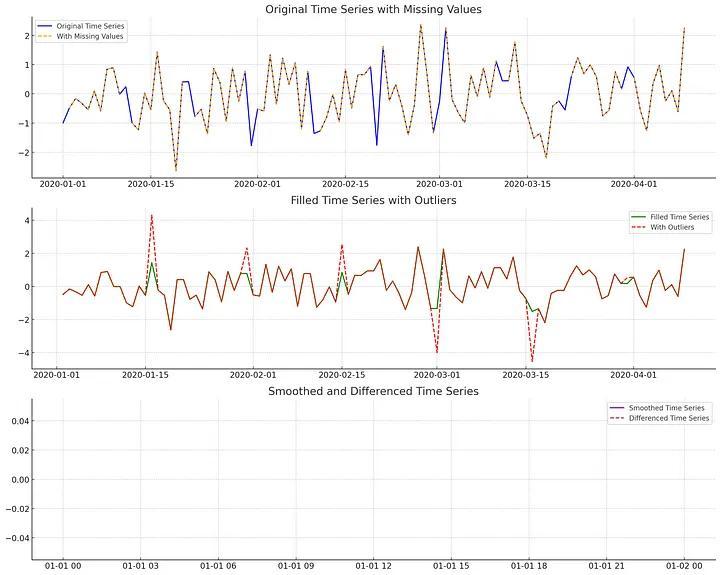
Xử lý dữ liệu bị thiếu hoặc dữ liệu ngoại lệ
- Dữ liệu bị thiếu:
- Xóa bỏ (Deletion): Đây là cách đơn giản nhất để xử lý khi có bản ghi không đầy đủ. Tuy nhiên, phương pháp này có thể dẫn tới mất mát thông tin hoặc làm giảm kích thước bộ dữ liệu.
- Điền dữ liệu (Imputation): Phương pháp này sẽ tiến hành điền TẤT CẢ chỗ bị thiếu dữ liệu bằng một giá trị được ước tính chung. Một vài phương pháp để ước tính giá trị đó là lấy trung bình (mean imputation), lấy trung vị (median imputation), …
- Nội suy (Interpolation): Phương pháp nội suy sẽ điền các giá trị bị khuyết bằng phương pháp nội suy như nội suy tuyến tính (linear interpolation)
- Một vài phương pháp khác như: Forward fill ( sử dụng giá trị ngay trước đó), Backward fill (sử dụng giá trị ngay sau đó)
- Loại bỏ ngoại lệ: phát hiện và xóa bỏ những ngoại lệ dữ liệu khỏi tập dữ liệu bằng cách sử dụng các phương pháp thống kê như Z-score hay IQR (Interqurtile Range)
Code python
# Handling missing values
time_series_with_nan = time_series.copy()
time_series_with_nan[::10] = np.nan # Introducing missing values
# Forward fill method
time_series_filled = time_series_with_nan.fillna(method='ffill')
# Detecting and removing outliers using Z-score
from scipy.stats import zscore
z_scores = zscore(time_series_filled)
abs_z_scores = np.abs(z_scores)
filtered_entries = (abs_z_scores < 3) # Z-score threshold
time_series_no_outliers = time_series_filled[filtered_entries]
Biến đổi dữ liệu (Transformation Data)
Biến đổi dữ liệu có thể giúp bạn xác định các khuôn mẫu (pattern) từ đó tạo cơ sở cho việc phân tích dữ liệu trở nên dễ dàng hơn
Có 3 phương pháp chính:
- Làm mượt dữ liệu (Smoothing): kĩ thuật như moving average có thể giúp làm giảm nhiễu cho dữ liệu
- Loại bỏ khác biệt (Differencing): Loại bỏ tính xu hướng / thời vụ bằng cách loại bỏ các giá trị trừng lặp
- Chuẩn hóa dữ liệu (Scaling and Normalization): Đảm bảo dữ liệu của bạn nằm trong một khoảng xác định
Code python
# Moving average smoothing
moving_avg = time_series_no_outliers.rolling(window=5).mean()
# Differencing
differenced_series = time_series_no_outliers.diff().dropna()
# Scaling
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_series = scaler.fit_transform(time_series_no_outliers.values.reshape(-1, 1))
Khám phá dữ liệu (Exploratory Data Analysis - EDA)
Trong phần này, chúng tả sẽ sử dụng các kĩ thuật khác nhau để hiểu và trực quan hóa dữ liệu.
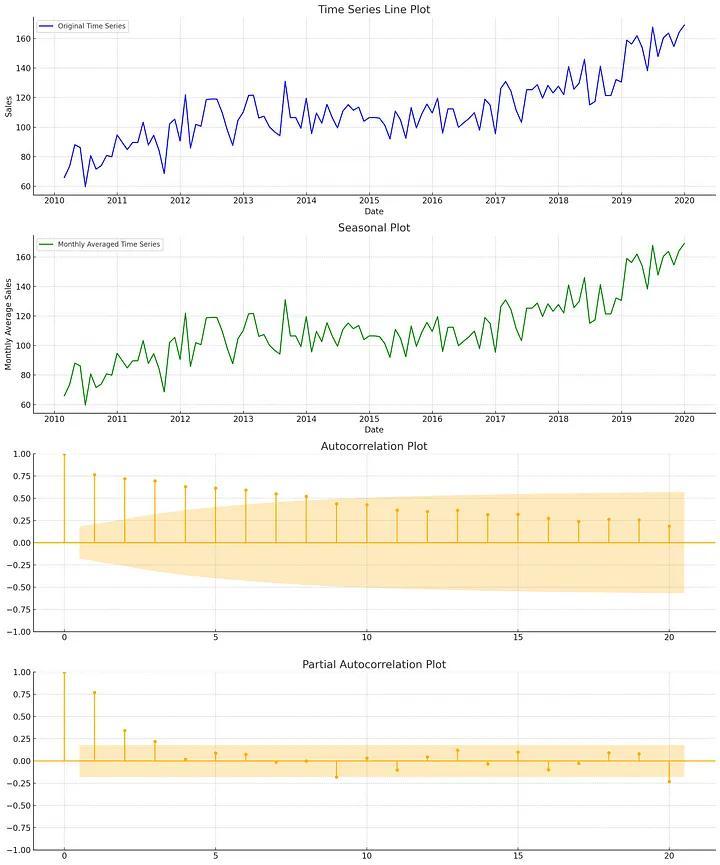
Trực quan hóa dữ liệu
Các biểu đồ thường dừng cho trực quan hóa dữ liệu:
- Biểu đồ đường (Line Plots): Phương pháp đơn giản nhất để trực quan hóa dữ liệu
- Biểu đồ thời vụ (Seasonal plots): để xác định khuôn mẫu mang tính thời vụ (seasonal patterns)
- Biểu đồ tương quan (Auto-correlation Plots): Kiểm tra sự tương quan của chuỗi với những giá trị trước đó
Code python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# I am Creating a realistic dummy time series dataset (e.g., monthly sales data over 10 years) to display the code execution
np.random.seed(0)
date_range = pd.date_range(start='1/1/2010', periods=120, freq='M')
trend = np.linspace(50, 150, 120) # Linear trend
seasonality = 10 + 20 * np.sin(np.linspace(0, 3.14 * 2, 120)) # Seasonal component
noise = np.random.normal(scale=10, size=120) # Random noise
data = trend + seasonality + noise
time_series = pd.Series(data, index=date_range)
# Handle missing values (if any)
time_series[::15] = np.nan
time_series = time_series.fillna(method='ffill')
# Moving average smoothing
moving_avg = time_series.rolling(window=12).mean()
# Differencing
differenced_series = time_series.diff().dropna()
# Preparing the data for seasonal plot
time_series_monthly = time_series.resample('M').mean()
# Plotting
plt.figure(figsize=(15, 18))
# Line plot
plt.subplot(4, 1, 1)
plt.plot(time_series, label='Original Time Series', color='blue')
plt.title('Time Series Line Plot')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.legend()
plt.grid(True)
# Seasonal plot
plt.subplot(4, 1, 2)
plt.plot(time_series_monthly, label='Monthly Averaged Time Series', color='green')
plt.title('Seasonal Plot')
plt.xlabel('Date')
plt.ylabel('Monthly Average Sales')
plt.legend()
plt.grid(True)
# Autocorrelation plot
plt.subplot(4, 1, 3)
cleaned_time_series = time_series.dropna()
plot_acf(cleaned_time_series, lags=20, ax=plt.gca())
plt.title('Autocorrelation Plot')
plt.grid(True)
# Partial autocorrelation plot
plt.subplot(4, 1, 4)
plot_pacf(cleaned_time_series, lags=20, ax=plt.gca())
plt.title('Partial Autocorrelation Plot')
plt.grid(True)
plt.tight_layout()
plt.savefig('./eda_visuals.png')
plt.show()
Phân tách dữ liệu chuỗi thời gian (Time Series Decomposition)
Để có thể hiểu được dữ liệu dạng chuỗi thời gian, bạn có thể phân tách dữ liệu (Decomposition) thành các thành phần đơn giản hơn, rồi từ đó bạn có thể đi sâu vào phân tích xu hướng hay khuôn mẫu của các thành phần.
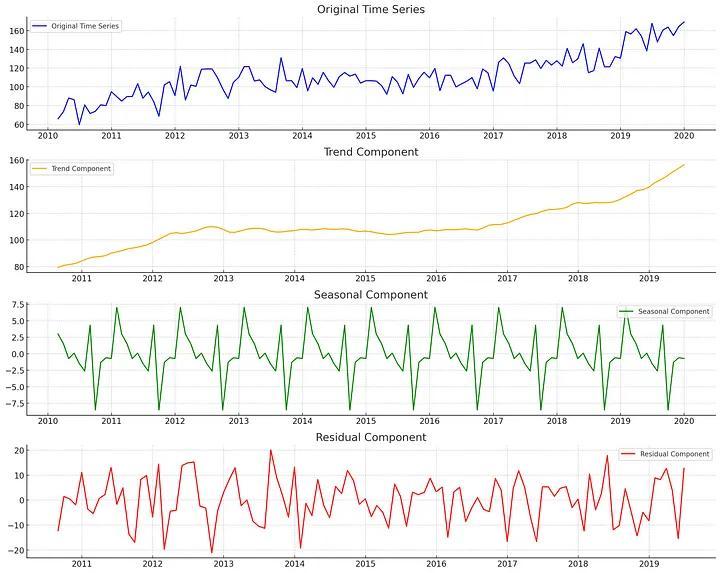
Các kĩ thuật phân tách
Có hai kĩ thuật phân tách chính
-
Mô hình cộng (Additive Model): Mô hình này giả thuyết rằng dữ liệu của bạn là dữ liệu được cộng từ nhiều thành phần khác nhau
Y(t)=T(t)+S(t)+R(t)Trong đó Y(t) là dữ liệu ban đầu, T(t) là thành phần dữ liệu xu hướng (trend component), S(t) là thành phần dữ liệu thời vụ (seasonal component) và R(t) là thành phần dư (Residual component)
-
Mô hình nhân (Multiplicative Model): Mô hình này giả thuyết rằng dữ liệu của bạn là kết quả của phép nhân từ nhiều thành phần khác nhau
Y(t)=T(t)*S(t)*R(t)
Code python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
# Creating a realistic dummy time series dataset (e.g., monthly sales data over 10 years)
np.random.seed(0)
date_range = pd.date_range(start='1/1/2010', periods=120, freq='M')
trend = np.linspace(50, 150, 120) # Linear trend
seasonality = 10 + 20 * np.sin(np.linspace(0, 3.14 * 2, 120)) # Seasonal component
noise = np.random.normal(scale=10, size=120) # Random noise
data = trend + seasonality + noise
time_series = pd.Series(data, index=date_range)
# Handle missing values (if any)
time_series[::15] = np.nan
time_series = time_series.fillna(method='ffill') # Forward fill missing values
# Ensure there are no remaining missing values
time_series = time_series.dropna()
# Decompose the time series
decomposition = seasonal_decompose(time_series, model='additive')
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
# Plotting the decomposed components
plt.figure(figsize=(15, 12))
plt.subplot(4, 1, 1)
plt.plot(time_series, label='Original Time Series', color='blue')
plt.title('Original Time Series')
plt.legend()
plt.subplot(4, 1, 2)
plt.plot(trend, label='Trend Component', color='orange')
plt.title('Trend Component')
plt.legend()
plt.subplot(4, 1, 3)
plt.plot(seasonal, label='Seasonal Component', color='green')
plt.title('Seasonal Component')
plt.legend()
plt.subplot(4, 1, 4)
plt.plot(residual, label='Residual Component', color='red')
plt.title('Residual Component')
plt.legend()
plt.tight_layout()
plt.savefig('/visuals/time_series_decomposition.png')
plt.show()
Mô hình dự đoán
Mô hình dự đoán là các mô hình có thể dự đoán các giá trị của chuỗi thời gian trong tương lai dựa vào chuỗi giá trị ở quá khứ. Có nhiều phương pháp để đạt được điều này từ phương pháp thống kê đơn thuần cho tới các kĩ thuật học máy nâng cao. Trong phần này, chúng ta sẽ đi qua một vài mô hình thông dụng để dự đoán chuỗi thời gian
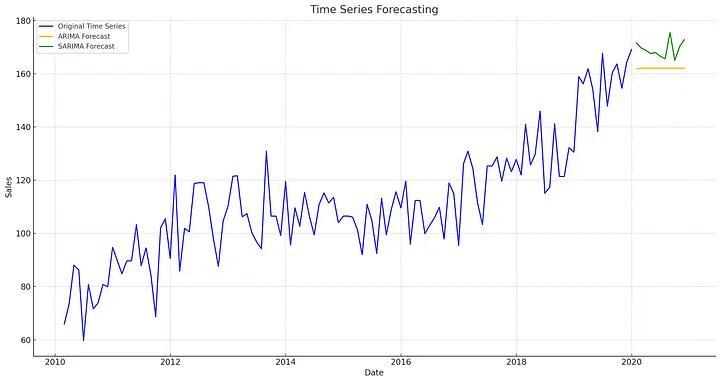
Phương pháp cổ điển
- Moving Average (MA)
- Autoregressive (AR) Models
- Autoregressive Integrated Moving Average (ARIMA)
Phương pháp nâng cao
- Seasonal ARIMA (SARIMA)
- Exponential Smoothing State Space Model (ETS)
Phương pháp học máy
- Hồi quy tuyến tính (Linear Regression)
- Cây quyết định và Rừng ngẫu nhiên (Decision Tree and Random Forests)
- Neural Networks (RNN, LSTM)
Code python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
# Creating a realistic dummy time series dataset (e.g., monthly sales data over 10 years)
np.random.seed(0)
date_range = pd.date_range(start='1/1/2010', periods=120, freq='M')
trend = np.linspace(50, 150, 120) # Linear trend
seasonality = 10 + 20 * np.sin(np.linspace(0, 3.14 * 2, 120)) # Seasonal component
noise = np.random.normal(scale=10, size=120) # Random noise
data = trend + seasonality + noise
time_series = pd.Series(data, index=date_range)
# Handle missing values (if any)
time_series[::15] = np.nan
time_series = time_series.fillna(method='ffill') # Forward fill missing values
# Ensure there are no remaining missing values
time_series = time_series.dropna()
# Fit ARIMA model
arima_model = ARIMA(time_series, order=(1, 1, 1))
arima_fit = arima_model.fit()
print(arima_fit.summary())
# Fit SARIMA model
sarima_model = SARIMAX(time_series, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
sarima_fit = sarima_model.fit(disp=False)
print(sarima_fit.summary())
# Forecasting with ARIMA
arima_forecast = arima_fit.get_forecast(steps=12)
arima_forecast_index = pd.date_range(start=time_series.index[-1], periods=12, freq='M')
arima_forecast_series = pd.Series(arima_forecast.predicted_mean, index=arima_forecast_index)
# Forecasting with SARIMA
sarima_forecast = sarima_fit.get_forecast(steps=12)
sarima_forecast_index = pd.date_range(start=time_series.index[-1], periods=12, freq='M')
sarima_forecast_series = pd.Series(sarima_forecast.predicted_mean, index=sarima_forecast_index)
# Plotting the original series and forecasts
plt.figure(figsize=(15, 8))
plt.plot(time_series, label='Original Time Series', color='blue')
plt.plot(arima_forecast_series, label='ARIMA Forecast', color='orange')
plt.plot(sarima_forecast_series, label='SARIMA Forecast', color='green')
plt.title('Time Series Forecasting')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.savefig('/visuals/time_series_forecasting.png')
plt.show()
Đánh giá và lựa chọn model
Để có thể lựa chọn được mô hình tốt nhất cho bài toán của mình, việc xây dựng một thước đo để đánh giá mức độ hiệu quả là điều vô cùng cần thiết. Dưới đây là một vài thước đo thường dùng
Hàm đánh giá (Evaluation Metrics)
- Mean Absolute Error (MAE): Đo trung bình sự khác biệt tuyệt đối giữa kết quả được dự đoán với số liệu thực thế
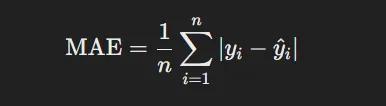
- Mean Squared Error (MSE): Tương tự với MAE, đo bình phương sự khác biệt giữa kết quả dự đoán với số liệu thực tế
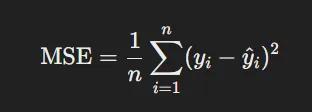
- Root Mean Squared Error (RMSE): Căn bặc hai của MSE
- Mean Absolute Percentage Error (MAPE): Đo trung bình sai số phần trăm lỗi
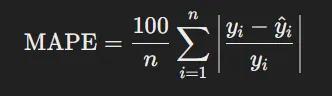
Code python
# Evaluation metrics
actual = time_series[-12:]
# ARIMA evaluation
arima_mae = mean_absolute_error(actual, arima_forecast_series[:12])
arima_mse = mean_squared_error(actual, arima_forecast_series[:12])
arima_rmse = np.sqrt(arima_mse)
arima_mape = np.mean(np.abs((actual - arima_forecast_series[:12]) / actual)) * 100
# SARIMA evaluation
sarima_mae = mean_absolute_error(actual, sarima_forecast_series[:12])
sarima_mse = mean_squared_error(actual, sarima_forecast_series[:12])
sarima_rmse = np.sqrt(sarima_mse)
sarima_mape = np.mean(np.abs((actual - sarima_forecast_series[:12]) / actual)) * 100
print(f"ARIMA MAE: {arima_mae}, MSE: {arima_mse}, RMSE: {arima_rmse}, MAPE: {arima_mape}")
print(f"SARIMA MAE: {sarima_mae}, MSE: {sarima_mse}, RMSE: {sarima_rmse}, MAPE: {sarima_mape}")
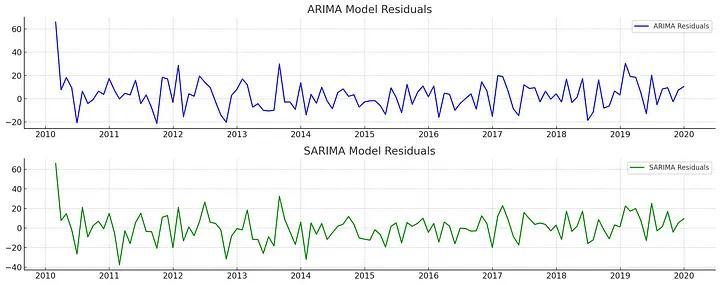
# Plotting the residuals
plt.figure(figsize=(15, 6))
plt.subplot(2, 1, 1)
plt.plot(arima_fit.resid, label='ARIMA Residuals', color='blue')
plt.title('ARIMA Model Residuals')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(sarima_fit.resid, label='SARIMA Residuals', color='green')
plt.title('SARIMA Model Residuals')
plt.legend()
plt.tight_layout()
plt.savefig('./visuals/model_evaluation_residuals.png')
plt.show()
ARIMA MAE: 6.740723561298947, MSE: 86.05719515259203, RMSE: 9.276701738904405, MAPE: nan
SARIMA MAE: 11.684219153028662, MSE: 195.5162161410725, RMSE: 13.982711330105921, MAPE: nan
Kết luận
Trong bài viết này, chúng ta đã đi qua sáu bước quan trọng trong phân tích dữ liệu chuỗi thời gian: từ định nghĩa và đặc điểm của dữ liệu chuỗi thời gian, các phương pháp tiền xử lý và làm sạch dữ liệu, kỹ thuật khám phá và trực quan hóa dữ liệu, cho đến phân tích, xây dựng mô hình dự đoán và cuối cùng là đánh giá, lựa chọn mô hình. Những bước này không chỉ giúp hiểu rõ hơn về dữ liệu mà còn cung cấp nền tảng để xây dựng các mô hình dự đoán chính xác và hiệu quả, áp dụng vào các dự án thực tế nhằm đạt kết quả tốt nhất. Hẹn gặp các bạn trong bài viết tới. 😄😄😄
Tài liệu tham khảo
https://www.kaggle.com/code/azminetoushikwasi/time-series-analysis-forecasting
All rights reserved
