Lược sử một số tên gọi trong Machine Learning & Deep Learning

Bài đăng này đã không được cập nhật trong 4 năm

1. Regression

Sau khi đọc lại rất nhiều lần bài viết này. Mình bắt đầu tự hỏi tại sao lại có cái tên regression (hồi quy). Cùng với việc tìm tòi wiki và những điều mình học hỏi được trong khóa học gần đây mình được tham gia; mình đã đúc kết ra được nguồn gốc của những cái tên sơ khai nhất trong Machine Learning.
Phân tích hồi quy (regression analysis) là một trong những phương pháp phổ biến nhất được sử dụng trong ngành thống kê phân tích dữ liệu. Thuật ngữ "regression" được định nghĩa bởi nhà Francis Galton. Ngài Francis Galton đã nghiên cứu và viết một số bài báo liên quan đến quá trình thừa kế trong đó ông quan sát và phát hiện một đặc tính trong mối liên hệ giữa chiều cao của thế hệ trước và chiều cao của thế hệ sau.

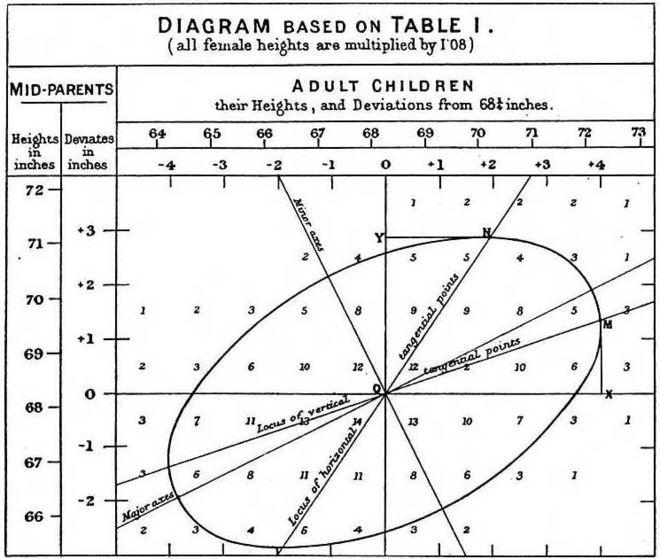
Theo lý thuyết di truyền học, thế hệ trước có chiều cao lớn hơn trung bình sẽ sản sinh ra thế hệ sau cũng cao hơn trung bình. Tuy nhiên Francis đã phát hiện ra rằng tỉ lệ cao hơn trung bình của thế hệ sau đã giảm so với thế hệ trước; đồng thời với các thế hệ sau có chiều cao thấp hơn trung bình lại có xu hướng ngược lại, tăng so với thế hệ trước.

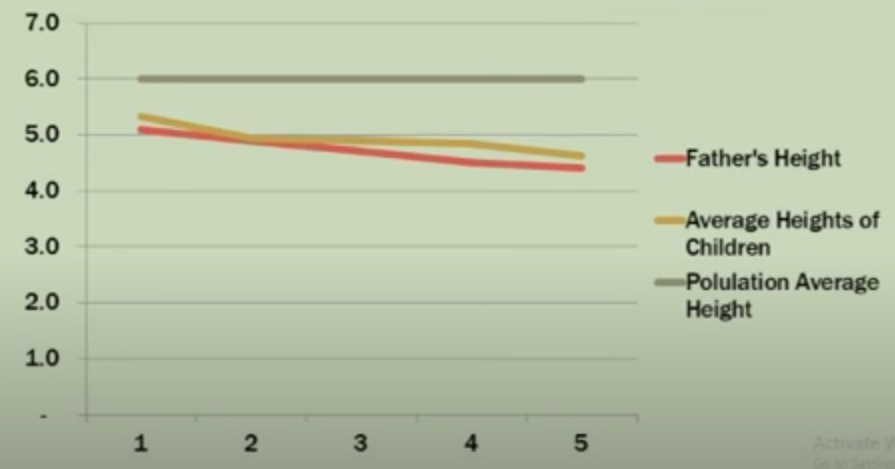
Ví dụ với thí nghiệm về cây hạt đậu của Galton:
Nếu cha (F1) có kích thước lớn hơn 1.5 lần mức trung bình thế hệ F1. Theo lý thuyết của Galton, con (F2) vẫn sẽ có kích thước lớn hơn mức trung bình thế hệ F2, tuy nhiên kích thước này sẽ có xu hướng nhỏ hơn con số 1.5 lần; và hoàn toàn ngược lại với các thế hệ F1 nhỏ hơn trung bình. Hiện tượng thú vị này được Galton gọi là Regression toward mean (hồi quy về trung bình), tức theo ông kích thước luôn luôn có xu hướng quay về mức trung bình. Khái niệm Regression ra đời từ đây

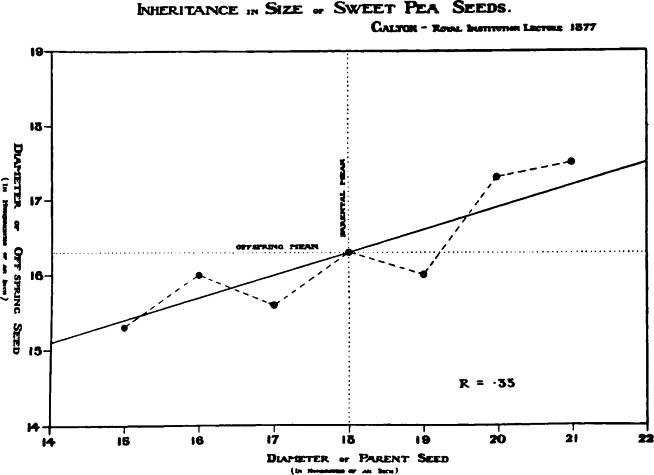
Hình trên là một trong những mô hình Linear regression đầu tiên được Galton sử dụng vào năm 1877 dựa trên nghiên cứu về kích thước hạt đậu

Cool fact:

Fact 1 - Francis Galton là em họ của Charles Darwin

Fact 2 - Thực tế, Francis Galton không phải là người đầu tiên ứng dụng mô hình Linear regression. Một trong những người sáng lập đầu tiên của mô hình regression là nhà toán học Carl-Friedrich Gauss. Gauss đã phát minh ra phương pháp least square (bình phương tối thiểu) để tính toán quỹ đạo của các hành tinh ứng dụng trong thiên văn học

Fact 3 - Các bạn có thể tham khảo và sử dụng Peas Dataset trong R

http://www.stat.uchicago.edu/~s343/Handouts/galton-peas.html https://www.picostat.com/dataset/r-dataset-package-psych-peas

2. Perceptron

Một trong những nền móng đầu tiên của neural network và deep learning là perceptron learning algorithm (hay perceptron). Perceptron là một thuật toán supervised learning giúp giải quyết bài toán phân lớp (classification) nhị phân, được khởi nguồn bởi Frank Rosenblatt trong một nghiên cứu của ông năm 1957. Thuật toán perceptron được chứng minh là hội tụ nếu hai lớp dữ liệu là linearly separable.

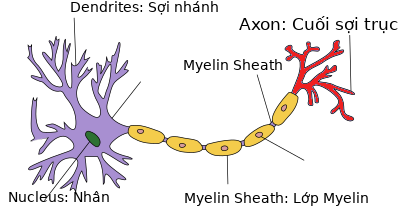
Ý tưởng của Perceptron được xây dựng dựa trên thần kinh neuron trong bộ não. Ở đầu neuron sẽ có chứa nhân, các tín hiệu đầu vào qua sợi nhánh (dendrites) và các tín hiệu đầu ra qua sợi trục (axon) kết nối với các neuron khác. Hiểu đơn giản mỗi nơ-ron nhận dữ liệu đầu vào qua sợi nhánh và truyền dữ liệu đầu ra qua sợi trục, đến các sợi nhánh của các nơ-ron khác.

Mỗi neuron nhận xung điện từ các nneuron khác qua sợi nhánh. Nếu các xung điện này đủ lớn để kích hoạt neuron, tín hiệu này đi qua sợi trục đến các sợi nhánh của các neuron khác

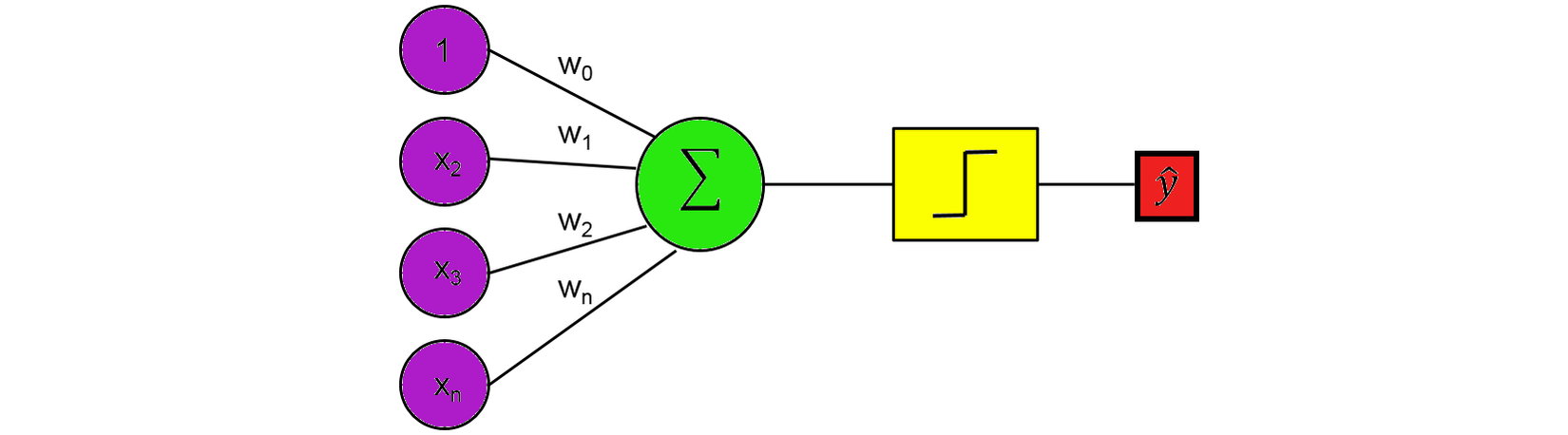
Single Layer Perceptron

Đây là perceptron một lớp. Nó cũng giống như tế bào thần kinh, có các đầu vào mà sau đó nhân với trọng số và tổng tất cả cùng nhau. Giá trị ở đây bây giờ được so sánh với threshold (ngưỡng )và sau đó được chuyển đổi bằng hàm activation (kích hoạt). Ví dụ, nếu tổng lớn hơn hoặc bằng 0, thì kích hoạt tức output ra 1; ngược lại, không kích hoạt hoặc output bằng 0.
Các đầu vào và trọng số w hoạt động giống như các chất dẫn truyền thần kinh trong một tế bào thần kinh, trong đó một số có thể dương và thêm vào tổng, và một số có thể âm và trừ khỏi tổng. Chức năng của Unit Step Function hoạt động như một ngưỡng của output.
Nếu ngưỡng được đáp ứng, sau đó chuyển tín hiệu, nếu không, tín hiệu sẽ không được truyền đi.

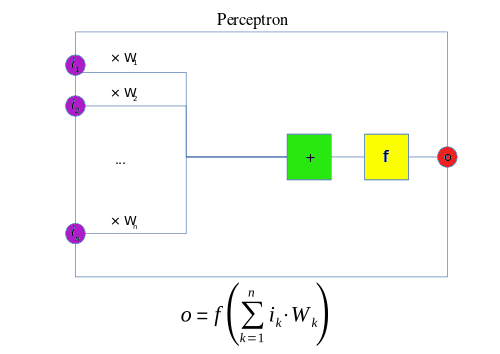
Mặc dù thuật toán này mang lại nhiều triển vọng, nó đã nhanh chóng được chứng minh không thể giải quyết những bài toán đơn giản. Năm 1969, Marvin Minsky và Seymour Papert trong cuốn sách nổi tiếng Perceptrons đã chứng minh rằng không thể "học" được hàm số XOR đơn giản khi sử dụng mạng perceptron.

3. Neural Network

Multi Layer Perceptron

Tín hiệu đầu ra các neuron trong não sẽ trở thành tín hiệu đầu vào cho neuron tiếp theo, từ đó hình thành các phản xạ điều khiển cơ thể của não bộ. Các hoạt động càng phức tạp càng cần sử dụng nhiều neuron hơn. Chính vì vậy việc hình thành 1 mạng nhiều lớp các single layter perceptron sẽ có được 1 mô hình học tốt hơn. Tuy nhiên, nếu kết hợp nhiều lớp perceptron với hàm activation mang tính linear thì lớp đầu ra vẫn mang tính linear, mô hình sẽ không học được gì nhiều chẳng khác gì single layer perceptron. Do đó, với MLP các hàm activation được lựa chọn là các hàm mang tính non-linear (sigmoid, tanh ...)

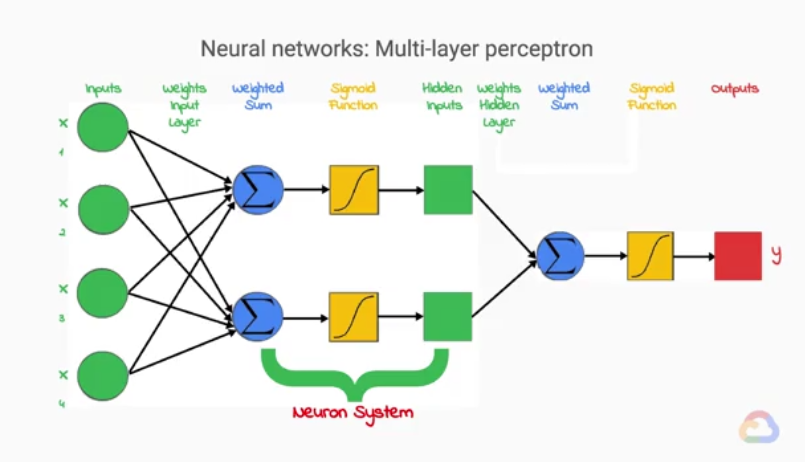
(Ảnh trên được trích nguồn từ khóa học Machine Learning with TensorFlow on Google Cloud Platform)
Mỗi output của một single layer perceptron sẽ thành input của single layer perceptron khác, và được gọi là Hidden inputs. Và Mình sẽ đi sâu hơn một chút về các layer này. Mỗi neuron chúng ta có thể hiểu là tập hợp của 3 bước: Tổng trọng số, hàm kích hoạt và output (hidden inputs). Và tập hợp chúng lại ta có 1 hidden layer

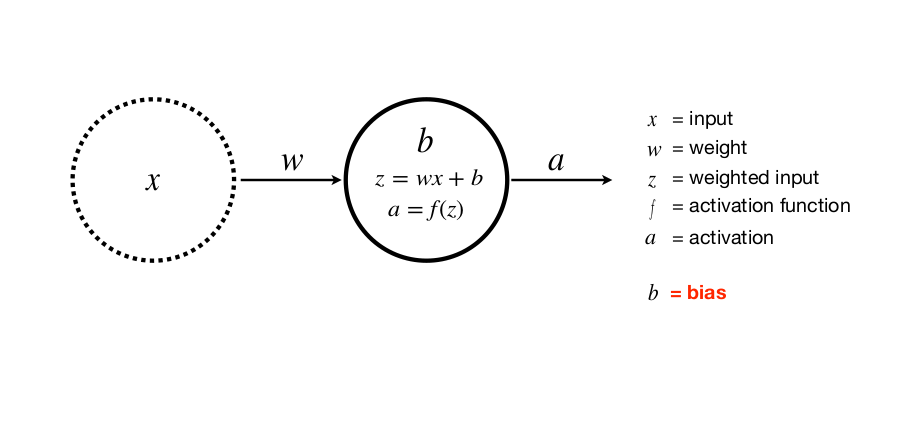
Với x là đầu vào, w là trọng số, z hay y là đầu ra, a là lớp activation với f là hàm activation

Ta có:
Một input, một lớp, một neuron (với b là bias). Việc thêm bias giúp tổng quát hóa phương trình đường thẳng, tránh trường hợp không tìm được phương trình mong muốn

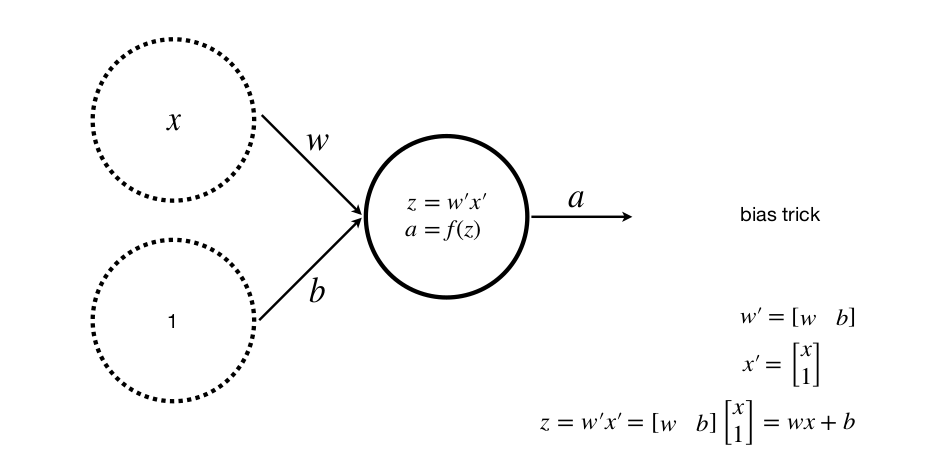
Nhiều input, một lớp, một neuron

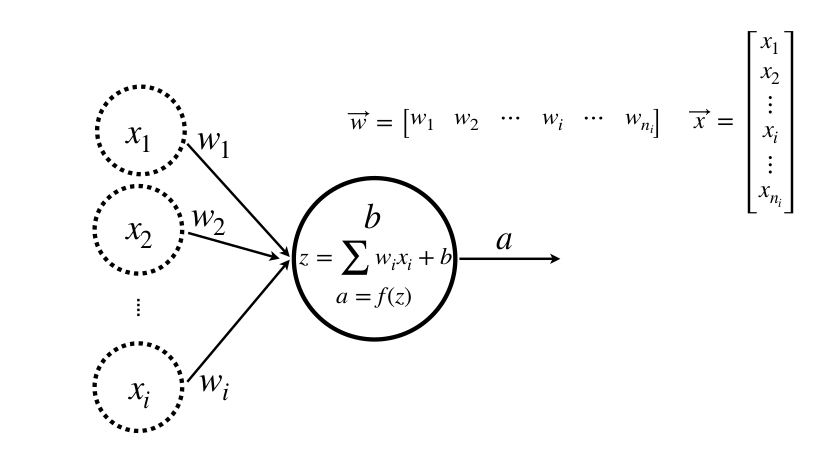
Nhiều Input, một lớp, nhiều neuron

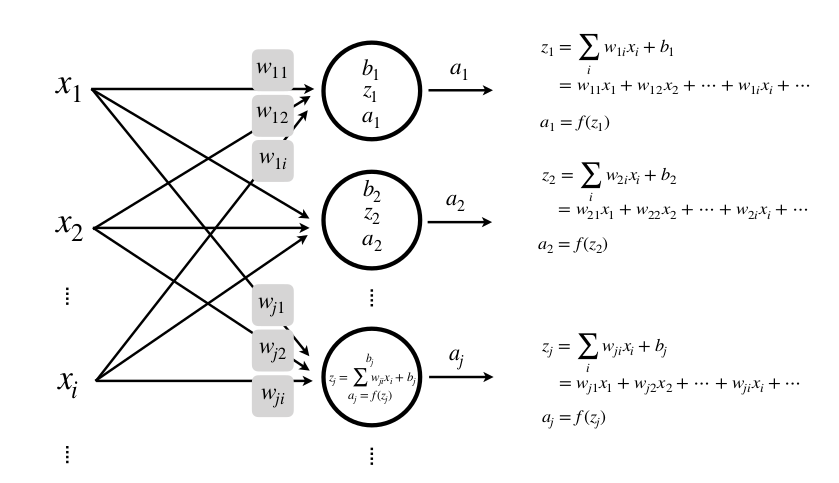
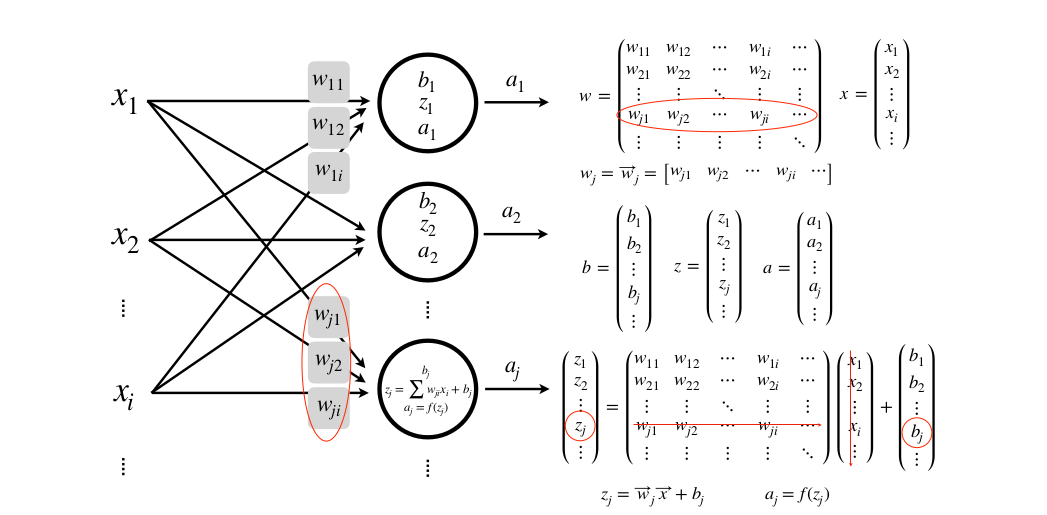
Nhiều input, nhiều lớp, nhiều neuron

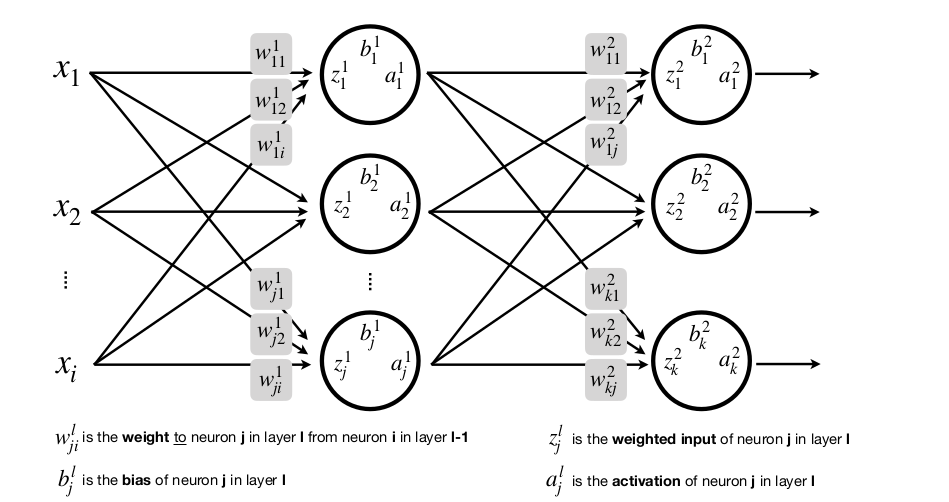
Và tưởng tượng nếu đầu vào X của bạn không phải là một vector mà là một ảnh dưới dạng ma trận thì sao. Phức tạp hơn nhiều rồi đúng không

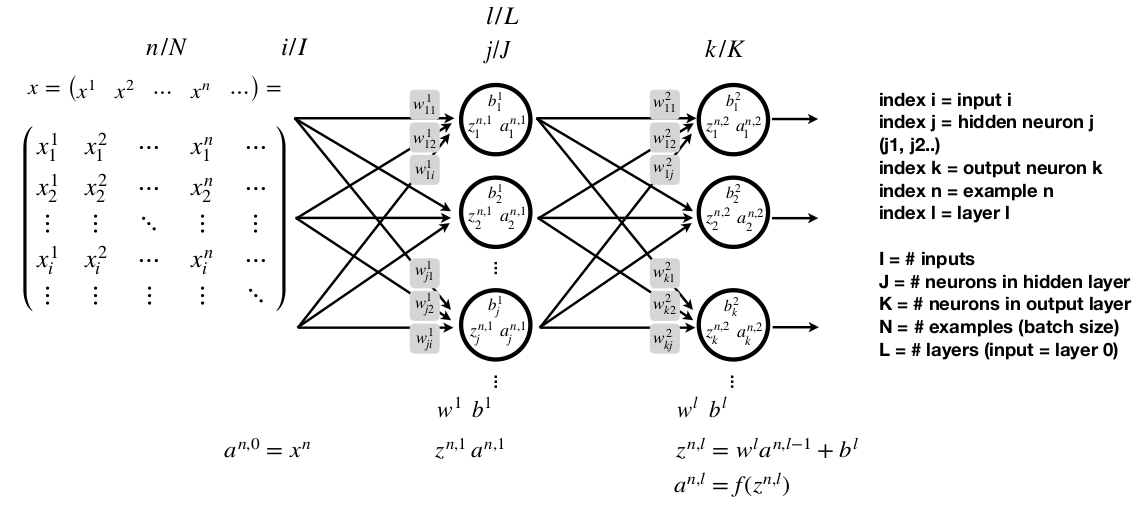
Với hidden layers, neural nets được chứng minh rằng có khả năng xấp xỉ hầu hết bất kỳ hàm số nào.
Tuy nhiên, với MLP một vấn đề vanishing gradient do giới hạn tính toán của máy tính thời đó cũng như hàm sigmoid.

Kết

Tìm hiểu về thế giới Machine Learning thật thú vị, mình luôn luôn có thắc mắc về nguồn gốc và cách hình thành của các kỹ thuật hiện nay. Các mạng hiện đại ngày nay với nhiều cải tiến hơn về khả năng tính toán, nguồn dữ liệu, hàm ReLU với cách tính và đạo hàm đơn giản giúp tốc độ huấn luyện tăng lên đáng kể, kỹ thuật Dropout được sử dụng để tăng tính generalization của model ... tuy nhiên vẫn được dựa trên cấu trúc Neural Network thời trước đó.