Giới thiệu về mô hình neural ODE

Ở bài trước, chúng ta đã tìm hiểu về một mô hình thời gian liên tục sử dụng SDE. Nếu chúng ta bỏ đi hệ số diffusion, phương trình này sẽ trở thành phương trình vi phân toàn phần theo thời gian $t$. Lúc này, việc thay đổi trạng thái sẽ trở nên tất định, do đó chúng ta có thể mô hình sự thay đổi của xác suất trạng thái theo thời gian, từ đó có thể mô hình một phiên bản tương tự của normalizing flow theo thời gian liên tục. Không chỉ vậy, cách làm này còn có thể sử dụng tương tự ResNet với kiến trúc bất kì.

ResNet và phương trình vi phân

Một mô hình ResNet về cơ bản có dạng sau

$$y_t=y_{t-1}+f_{t-1}(y_{t-1})$$

với $t\in\{1,2,...,T\}$, $y_{t}, f_{t}$ là đầu vào và biến đổi ở lớp thứ $t$. Nếu chúng ta coi $t$ là chuỗi số thực $\{t_1, t_2, ..., t_T\}$, chúng ta có thể viết lại thành

$$y_{t_i}=y_{t_{i-1}}+(t_i-t_{i-1})f_{t_{i-1}}(y_{t_{i-1}}).$$

Đây chính là cách xấp xỉ một phương trình vi phân bằng phương pháp Euler. Cụ thể hơn, khi $T\to\infty$, cách làm này xấp xỉ phương trình sau

$$\frac{dy_t}{dt}=f(t, y_t)$$

Từ góc nhìn này, ta có thể xem mạng neural như một quá trình thay đổi của một trạng thái $y_t$ theo thời gian, biểu diễn bởi phương trình vi phân (ordinary differential equation - ODE) như trên thay vì mô hình theo từng lớp như truyền thống. Đầu ra của mô hình sẽ là trạng thái tại thời điểm $T$, được tìm bằng cách giải ODE với điều kiện đầu là đầu vào $y_0$. Mô hình này có thể sử dụng để thay thế bất kì mô hình ResNet nào. Hàm $f$ ở đây có thể là một kiến trúc tùy ý, nhận trạng thái $y$ và thời gian $t$, trả về vector cùng chiều với $y$.

Một tính chất quan trọng của ODE là liệu từ phương trình này có thể xác định được $y_t$ không. Định lý Picard–Lindelöf chỉ ra rằng trong trường hợp $f$ là Lipschitz theo $y$, tồn tại $\epsilon$ sao cho $y(t)$ tồn tại và xác định duy nhất quanh $[-\epsilon, \epsilon]$. Như vậy, để ODE định nghĩa tốt, chúng ta cần mô hình thỏa mãn tính chất Lipschitz.

Giải ODE

Với ODE với điều kiện đầu $y_0$ bên trên, trạng thái tại thời điểm $t$ sẽ được tính như sau

$$y_t = y_0 + \int_0^t f(\tau, y_\tau)d\tau$$

Mục tiêu của chúng ta sẽ là xấp xỉ tích phân trên. Cách đơn giản nhất là phương pháp Euler: Với mỗi chuỗi $t_0<t_1<...<t_T$, chúng ta tính lần lượt $T$ giá trị tại những thời điểm trên như sau:

$$y_i = y_{i-1} + h\cdot f(t_{i-1}, y_{i-1}),\quad h=t_i-t_{i-1}$$

Như đã nói ở trên, cách làm này giống với mô hình ResNet quen thuộc.

def odeint_euler(f, y0, t):
  def step(state, t):
    y_prev, t_prev = state
    dt = t - t_prev
    y = y_prev + dt * f(t_prev, y_prev)
    return y, t
  t_curr = t[0]
  y_curr = y0
  ys = []
  for i in t[1:]:
    y_curr, t_curr = step((y_curr, t_curr), i)
    ys.append(y_curr)
  return torch.stack(ys)

Một cách xấp xỉ phổ biến khác có sai số thấp hơn là phương pháp Runge-Kutta, xấp xỉ sai khác giữa các thời điểm bởi 4 giá trị

$$y_i = y_{i-1}+\frac{h}{6}(k_1+2k_2+2k_3+k_4)$$

$$\begin{aligned} k_1 &=f(t_{i-1}, y_{i-1})\\ k_2 &=f(t_{i-1}+\frac{h}{2}, y_{i-1}+h\frac{k_1}{2})\\ k_3 &=f(t_{i-1}+\frac{h}{2}, y_{i-1}+h\frac{k_2}{2})\\ k_4&=f(t_{i-1}+h, y_{i-1}+hk_3) \end{aligned}$$

def odeint_rk4(f, y0, t):
  def step(state, t):
    y_prev, t_prev = state
    dt = t - t_prev
    k1 = dt * f(t_prev, y_prev)
    k2 = dt * f(t_prev + dt/2., y_prev + k1/2.)
    k3 = dt * f(t_prev + dt/2., y_prev + k2/2.)
    k4 = dt * f(t + dt, y_prev + k3)
    y = y_prev + (k1+ 2 * k2 + 2 * k3 + k4) / 6
    return y, t
  t_curr = t[0]
  y_curr = y0
  ys = []
  for i in t[1:]:
    y_curr, t_curr = step((y_curr, t_curr), i)
    ys.append(y_curr)
  return torch.stack(ys)

Tính thử một ví dụ với ODE sau

$$\frac{dy_t}{dt}=y_t,\quad y_0=2$$

ODE có nghiệm là $y_t=y_0e^t$. Dùng $100$ bước để xấp xỉ tích phân để tính $y_{10}$, hai cách tính trên cho kết quả như bên dưới

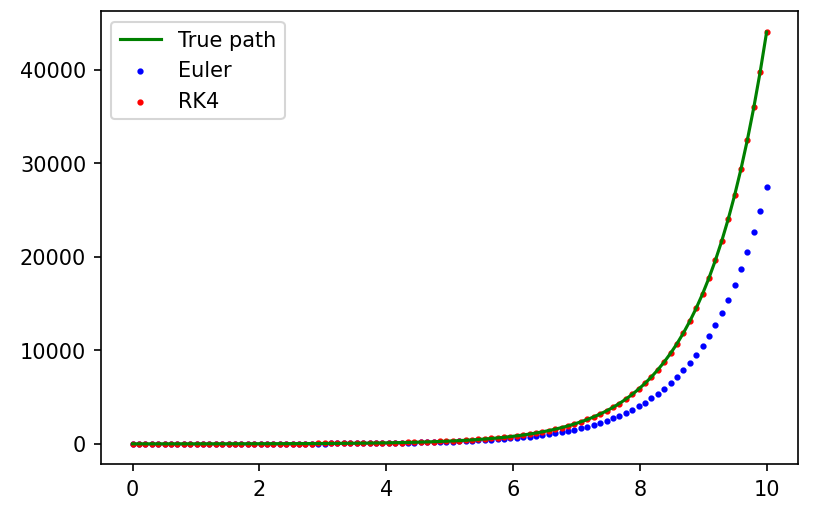
Ta có thể thấy phương pháp Euler cho kết quả không chính xác. Điều này thể hiện khoảng cách giữa các bước ảnh hưởng đến độ chính xác của phương pháp xấp xỉ. Do đó ta có thể xấp xỉ ODE chính xác hơn bằng cách chọn độ dài mỗi bước sao cho ước lượng lỗi tối ưu (việc này yêu cầu một cách để ước lượng lỗi, ví dụ như dùng một phương pháp khác để xấp xỉ, rồi tính sai khác giữa kết quả của hai phương pháp). Tuy nhiên điều này nảy sinh một vấn đề sau: Trong trường hợp ta muốn dùng minibatch, sai số giữa các ODE trong batch là khác nhau, do đó thời gian giữa các ODE sẽ khác nhau, việc xử lý toàn batch sẽ không giống như mạng neural thông thường. Một cách giải quyết là gộp chung toàn batch thành 1 ODE, các mốc thời gian sẽ dùng chung, tuy nhiên có thể tăng sai số. Đối với jax, ta có thể dùng vmap để tính song song các ODE trong batch (gần đây torch cũng có cài đặt vmap).

Cập nhật tham số

Ở bài trước, chúng ta đã làm quen với một mô hình thời gian liên tục với SDE bằng mô hình trực tiếp score theo thời gian. Tuy nhiên, đối với neural ODE, ta đang mô hình sự thay đổi của trạng thái theo thời gian. Do đó việc cập nhật gradient trở nên không hiển nhiên, yêu cầu tham số hóa lại đối với tham số của mô hình.

Phần này sẽ trình bày cách cập nhật gradient cho hai cách cài đặt automatic differentiation là tích vector-Jacobian (VJP) và tích Jacobian-vector (JVP). Chi tiết về hai cách cài đặt này có thể xem ở tài liệu tham khảo của thư viện jax.

Tính với tích vector-Jacobian (reverse mode)

Để cho thuận tiện, chúng ta sẽ viết lại phương trình vi phân dưới dạng sau

$$\frac{\partial y(t, y_0, \theta)}{\partial t} = f(t, y(t, y_0, \theta), \theta))$$

Giả sử hàm mục tiêu được tính tại trạng thái cuối $y_T$ tại thời điểm $y_T$ thông qua hàm $L(y_T,\theta)$, từ định lí tồn tại duy nhất hàm này cũng có thể được tính từ trạng thái $y_t$ thông qua hàm $L_t(y_t,\theta)$.

Mục tiêu của chúng ta là đạo hàm đối với trạng thái ban đầu $y_0$ và tham số $\theta$, nói cách khác là tính đạo hàm riêng $\frac{\partial L_0(y_0,\theta)}{\partial y_0}$ và $\frac{\partial L_0(y_0,\theta)}{\partial \theta}$.

Đặt

$$a(t,y_0,\theta) = \frac{\partial L_t(y_t,\theta)}{\partial y_t},$$

chúng ta đã biết $a(T, y_0,\theta)$ và cần tính $a(0,y_0,\theta)$. Như vậy, chúng ta có thể mô hình sự thay đổi $\frac{\partial a(t, y_0,\theta)}{\partial t}$ của hàm $a$ theo thời gian $t$, từ đó tính ra $a(0,y_0,\theta)$ bằng cách tích phân theo thời gian từ $T$ về $0$.

Do ODE có nghiệm duy nhất xung quanh lân cận của $y_0$, ta có thể lấy đạo hàm riêng theo $y_0$ tại hai vế

$$\frac{\partial^2 y(t, y_0, \theta)}{\partial y_0\partial t} = \frac{\partial f(t, y(t, y_0, \theta), \theta))}{\partial y_0}$$

Đổi thứ tự đạo hàm riêng và áp dụng chain rule ta có

$$\frac{\partial^2 y(t, y_0,\theta)}{\partial t\partial y_0}=\frac{\partial f(t, y, \theta)}{\partial y}\frac{\partial y(t,y_0,\theta)}{\partial y_0}.$$

Quay lại với hàm mục tiêu, áp dụng chain rule ta được

$$\frac{\partial L_0(y_0,\theta)}{\partial y_0} = \frac{\partial L_t(y_t,\theta)}{\partial y_t}\frac{\partial y(t,y_0,\theta)}{\partial y_0}$$

Từ hai điều trên, ta có thể mô hình sự thay đổi của $a(t, y_0,\theta)$ theo thời gian như sau

$$\frac{\partial a(t,y_0, \theta)}{\partial t} = - a(t,y_0,\theta)\frac{\partial f(t,y,\theta)}{\partial y}$$

Lúc này $a(0, y_0,\theta)$ có thể tính bởi

$$a(0, y_0,\theta) = a(T,y_0,\theta)-\int_T^0 a(t,y_0,\theta)\frac{\partial f}{\partial y} dt$$

Để tính $a(t,\theta)\frac{\partial f}{\partial y}$, chúng ta sẽ dùng vector-Jacobian với đầu vào là $y$. Trạng thái này có thể được tính lại bằng ODE ban đầu.

Tiếp theo chúng ta sẽ tính đạo hàm riêng với tham số của mô hình, áp dụng chain rule ta được

$$\frac{\partial L_0(y_0,\theta)}{\partial \theta} = \frac{\partial L_t(y_t,\theta)}{\partial y_t} \frac{\partial y_t}{\partial \theta}+\frac{\partial L_t(y_t,\theta)}{\partial \theta}$$

Tương tự như trên, nếu chúng ta có thể mô hình được sự thay đổi của $b(t, y_0,\theta)=\frac{\partial L_t(y_t,\theta)}{\partial \theta}$ theo thời gian, $b(0,y_0,\theta)=\frac{\partial L_0(y_0,\theta)}{\partial \theta}$ có thể tính bằng cách tích phân từ trạng thái $\frac{\partial L_T(y_T,\theta)}{\partial \theta}$.

Lấy đạo hàm theo $t$ ở hai vế, ta có

$$\frac{\partial a(t, y_0,\theta)}{\partial t}\frac{\partial y}{\partial \theta}+a(t,y_0,\theta)\frac{\partial^2 y}{\partial t\partial \theta}+\frac{\partial b(t,y_0,\theta)}{\partial t} = 0$$

Tương tự như trạng thái đầu $y_0$, ta có thể giả sử ODE thỏa mãn quanh lân cận của $\theta$ và lấy đạo hàm theo $\theta$ ở hai vế, sau đó đổi thứ tự đạo hàm và áp dụng chain rule

$$\frac{\partial^2 y(t, y_0,\theta)}{\partial t\partial \theta}=\frac{\partial f(t, y, \theta)}{\partial y}\frac{\partial y(t,y_0,\theta)}{\partial \theta} + \frac{\partial f(t,y,\theta)}{\partial \theta}.$$

Thay $\frac{\partial a}{\partial t}$ và $\frac{\partial^2y}{\partial t\partial \theta}$, ta được

$$-a(t,y_0,\theta)\frac{\partial f(t,y,\theta)}{\partial y}\frac{\partial y(t,y_0,\theta)}{\partial \theta}+a(t,y_0,\theta)\left(\frac{\partial f(t, y, \theta)}{\partial y}\frac{\partial y(t,y_0,\theta)}{\partial \theta} + \frac{\partial f(t,y,\theta)}{\partial \theta}\right)+\frac{\partial b(t,y_0,\theta)}{\partial t} = 0$$

Suy ra

$$\frac{\partial b(t,y_0,\theta)}{\partial t} = -a(t,y_0,\theta)\frac{\partial f(t,y,\theta)}{\partial \theta}.$$

Một câu hỏi nữa là giá trị của điều kiện đầu là gì. Chúng ta có thể nhận ra hàm mất mát được tính dựa trên trạng thái cuối $y_T$ mà không cần đến tham số của quá trình, do đó $b(T,y_0,\theta)=\frac{\partial L(y_T,\theta)}{\partial \theta}=0$.

Từ đây ta có thể tính được

$$\frac{\partial L_0(y_0,\theta)}{\partial \theta}=b(0,y_0,\theta)=-\int_T^0 a(t,y_0,\theta)\frac{\partial f(t,y,\theta)}{\partial \theta}dt.$$

Tổng hợp lại, để tìm đạo hàm riêng theo trạng thái ban đầu và tham số của mô hình, ta sẽ giải hệ phương trình vi phân sau

$$d\begin{bmatrix} y_t \\ a_t \\ b_t \end{bmatrix} = \begin{bmatrix} f(t,y,\theta)\\ -a_t\frac{\partial f}{\partial y}\\ -a_t\frac{\partial f}{\partial \theta} \end{bmatrix}dt$$

với trạng thái ban đầu là

$$\begin{bmatrix} y_T \\ a_T \\ b_T \end{bmatrix}=\begin{bmatrix} y_T\\ \frac{d L(y_T)}{d y_T}\\ 0 \end{bmatrix}$$

Ghi chú: Với cách cài đặt này , ta phải tích phân ngược theo thời gian. Điều này yêu cầu phương pháp xấp xỉ ODE phải thỏa mãn tính chất thời gian khả nghịch, cụ thể hơn khi giải ODE theo chiều thuận rồi từ đó giải theo chiều nghịch, ta được chính xác điều kiện đầu. Các phương pháp giải ODE bậc nhất (bao gồm phương pháp Euler, Runge-Kutta) không thoả mãn tính chất này.

Tính với tích Jacobian-vector (forward mode)

Đối với cách cài đặt này, ta quan tâm đến phép pushforward từ $y_0$ và $\theta$ sang $y_T$. Ta có

$$\Delta y_t = \frac{\partial y(t, y_0,\theta)}{\partial y_0}\Delta y_0 + \frac{\partial y(t, y_0,\theta)}{\partial \theta}\Delta \theta$$

với mọi $t$ ($\Delta y_0, \Delta \theta, \Delta y_t$ kí hiệu vector tiếp tuyến tại $y_0,\theta$ và vector tiếp tuyến tương ứng tại $y_t$, đại diện cho sự thay đổi tại $y_0, \theta, y_t$). Tương tự phần trên, ta nghĩ đến việc tìm sự thay đổi của $\Delta y_t$ theo thời gian.

$$\frac{d}{dt}\Delta y_t= \frac{\partial^2 y(t, y_0,\theta)}{\partial t\partial y_0}\Delta y_0 + \frac{\partial^2 y(t, y_0,\theta)}{\partial t\partial \theta}\Delta \theta.$$

Đặt $u(t, y_0, \theta, \Delta y_0)=\frac{\partial y(t, y_0,\theta)}{\partial y_0}\Delta y_0, v(t,y_0, \theta, \Delta \theta) = \frac{\partial y(t, y_0,\theta)}{\partial \theta}\Delta \theta$. Ở phần trên chúng ta đã có

$$\frac{\partial u}{\partial t}=\frac{\partial f}{\partial y}u$$

$$\frac{\partial v}{\partial t}=\frac{\partial f}{\partial y}v + \frac{\partial f}{\partial \theta}\Delta \theta$$

Do đó

$$\frac{\partial (u+v)}{\partial t}=\frac{\partial f}{\partial y}(u+v) + \frac{\partial f}{\partial \theta}\Delta \theta$$

Việc còn lại là tìm điều kiện đầu. Tại thời điểm $0$, $y=y_0$, do vậy $u(0)=\Delta y_0, v(0)=0$. Lúc này việc tìm vi phân tại $y_T$ tương đương với việc giải ODE

$$\frac{d}{dt}w_t=\frac{\partial f}{\partial y}w_t + \frac{\partial f}{\partial \theta}\Delta \theta$$

với điều kiện đầu $w_0=\Delta y_0$.

Ví dụ

Trong phần này mình sẽ minh họa với pytorch, sử dụng hàm vjp và jvp. Hai hàm này nhận vào một hàm bất kì có đầu vào và đầu ra là tensor, rồi tính VJP/JVP tại đầu vào theo một vector tiếp tuyến nào đó.

Đối với VJP/JVP theo tham số của mô hình, chúng ta có thể xóa attribute rồi đặt lại để đưa tham số vào đối số của hàm forward, xem cụ thể tại đây

def del_attr(obj, names):
    if len(names) == 1:
        delattr(obj, names[0])
    else:
        del_attr(getattr(obj, names[0]), names[1:])
def set_attr(obj, names, val):
    if len(names) == 1:
        setattr(obj, names[0], val)
    else:
        set_attr(getattr(obj, names[0]), names[1:], val)

def make_functional(mod):
    orig_params = tuple(mod.parameters())
    names = []
    for name, p in list(mod.named_parameters()):
        del_attr(mod, name.split("."))
        names.append(name)
    return orig_params, names

def load_weights(mod, names, *params):
    for name, p in zip(names, params):
        set_attr(mod, name.split("."), p)

def del_weights(mod):
    for name, p in list(mod.named_parameters()):
        del_attr(mod, name.split("."))
        
class Model(nn.Module):
  def __init__(self):
    super(Model, self).__init__()
    self.module = nn.Sequential(nn.Linear(4, 5), nn.LeakyReLU(), nn.Linear(5,3),nn.Tanh())

  def get_params(self):
    self.params, self.names = make_functional(self)

  def forward(self, t, state, *args):
    if len(args) == 0:
      load_weights(self, self.names, *self.params)
    elif len(args) > 0:
      del_weights(self)
      load_weights(self, self.names, *args)
    return self.module(torch.cat([t.view(1), state]))

model = Model()
model.get_params()

Khi tính JVP/VJP, chúng ta cần giải hệ ODE, do đó thuật toán cần được chỉnh sửa một chút

def odeint_rk4_system(f, y0, t):
  """
    y0 : list of states
    f : func returns list of states
  """
  def step(state, t):
    y_prev, t_prev = state
    dt = t - t_prev
    k1 = [dt * i for i in f(t_prev, y_prev)]
    k2 = [dt * i for i in f(t_prev + dt/2., [y + j1/2. for y, j1 in zip(y_prev, k1)])]
    k3 = [dt * i for i in f(t_prev + dt/2., [y + j2/2. for y, j2 in zip(y_prev, k2)])]
    k4 = [dt * i for i in f(t + dt, [y + j3 for y, j3 in zip(y_prev, k3)])]
    y = [i + (j1+ 2 * j2 + 2 * j3 + j4) / 6 for i, j1, j2, j3, j4 in zip(y_prev, k1, k2, k3, k4)]
    return y, t
  t_curr = t[0]
  y_curr = y0
  ys = []
  for i in t[1:]:
    y_curr, t_curr = step((y_curr, t_curr), i)
    ys.append(y_curr)
  return ys

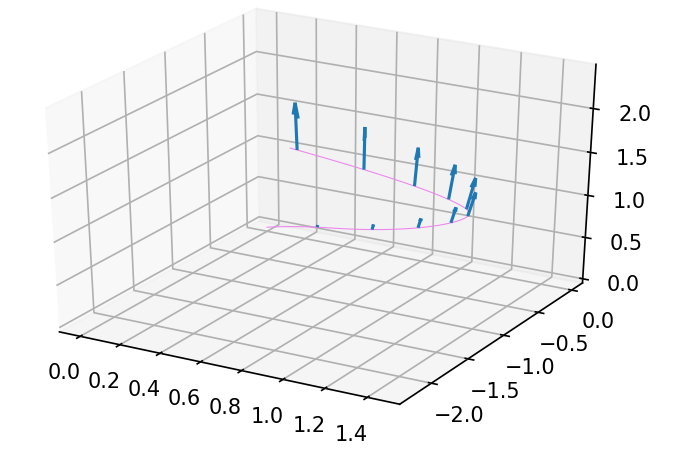
Chúng ta sẽ mô hình đạo hàm theo thời gian của vị trí 1 điểm trong $\mathbb{R}^3$ với phương pháp Runge-Kutta bậc 4, được kết quả như hình dưới

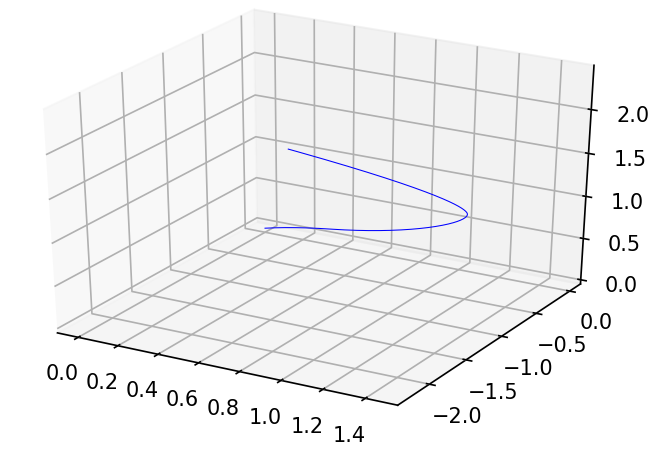
Với vector tiếp tuyến $[0, 0, 1]$ tại điều kiện đầu, pushforward theo thời gian được vector tiếp tuyến tại từng thời điểm như sau

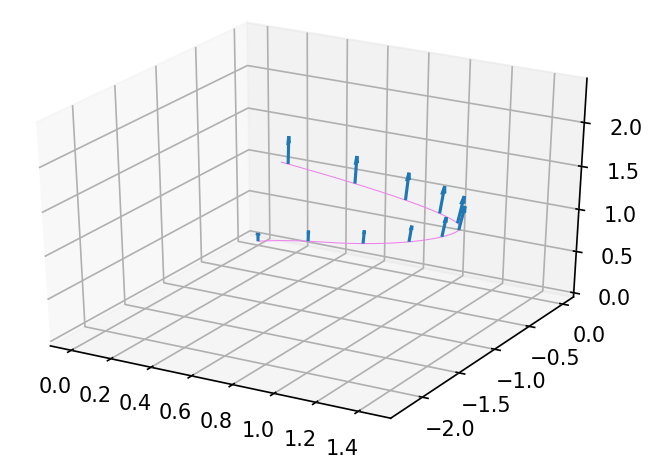
Với vector tiếp tuyến $[0, 0, 1]$ tại $T$, chúng ta kéo lùi lại $y_0$ và $\theta$. Áp dụng JVP với $dy_0$ được kết quả như hình

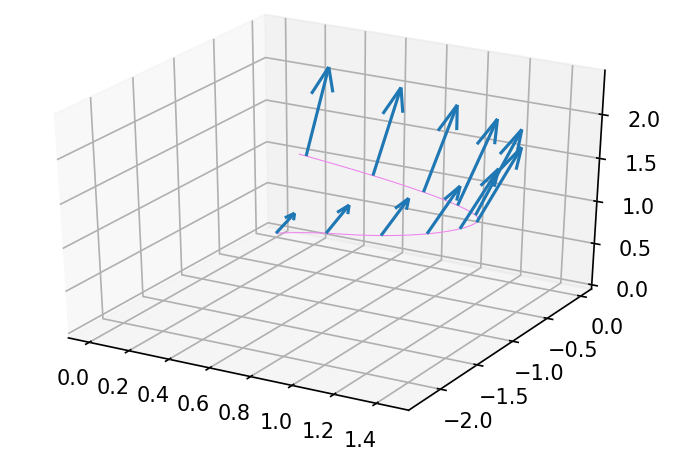
Áp dụng JVP với $d\theta$ được kết quả sau

Code sử dụng trong bài có thể xem ở đây.

Trong bài tiếp theo, chúng ta sẽ tìm hiểu về mô hình continuous normalizing flow với neural ODE, và liên hệ với SDE ở bài trước.

Tham khảo

• Neural Ordinary Differential Equations
• NeuRIPS Tutorials on Implicit deep learning
• Julia lib