[B5'] EAD: Elastic-Net Attacks to Deep Neural Networks via Adversarial Examples

Đây là một bài trong series Báo khoa học trong vòng 5 phút.

Nguồn

Được viết bởi Chen et. al, IBM. Được đăng ở AAAI '18.
https://www.aaai.org/ocs/index.php/AAAI/AAAI18/paper/viewFile/16893/15665

Ý tưởng chính

Thay vì sử dụng $l_2$ như Carlini-Wagner (CW), hay $l_\infty$ như PGD, thì tác giả sử dụng kết hợp giữa $l_1$ và $l_2$ tương tự với Elastic-Net Regularization. Cụ thể, mục đích tối thượng là tối ưu hàm loss sau:

$$\min_\mathbf{x}c\cdot f(\mathbf{x},t)+\beta\Vert \mathbf{x}-\mathbf{x}_0\Vert_1+\Vert\mathbf{x}-\mathbf{x}_0\Vert_2^2,$$

trong đó $f(\mathbf{x}, t)$ được định nghĩa là độ thành công của tấn công, với giá trị bé hơn 0 là thành công, và ngược lại. Công thức của $f(\mathbf{x},t)$ cho targeted attack tới class $t$ là

$$f(\mathbf{x}, t)=\max\{\max_{j\ne t}[\mathbf{Logit}(\mathbf{x})]_j-[\mathbf{Logit}(\mathbf{x})]_t-\kappa\},$$

với Logit là giá trị vector ngay trước softmax, $\kappa$ là độ "an toàn" của tấn công, còn phiên bản untargeted với true label $t_0$ là

$$f(\mathbf{x})=\max\{[\mathbf{Logit}(\mathbf{x})]_{t_0}-\max_{j\ne t_0}[\mathbf{Logit}(\mathbf{x})]_j-\kappa\}.$$

$\kappa$ càng tăng thì độ an toàn của tấn công càng lớn, và các adversarial example này sẽ càng có khả năng transfer — chúng có thể được sử dụng trên một model khác train cùng task cùng data.

Sau đó, tác giả tối ưu hóa hàm này bằng FISTA (phiên bản nhanh hơn của ISTA, mà không sử dụng SGD). Thay vì tối ưu cả hàm $f$ phức tạp, chúng ta chỉ tối ưu hàm $g$ không có term $l_1$-norm

$$g(\mathbf{x})=c\cdot f(\mathbf{x},t)+\Vert\mathbf{x}-\mathbf{x}_0\Vert_2^2$$

và sử dụng projected shrinkage-thresholding:

$$[S_\beta(\mathbf{z})]_i=\begin{cases} \min\{\mathbf{z}_i-\beta, 1\}& \text{ if } \mathbf{z}_i - \mathbf{x}_{0i} > \beta;\\ \mathbf{x}_{0i}& \text{ if } |\mathbf{z}_i - \mathbf{x}_{0i}| \le \beta;\\ \max\{\mathbf{z}_i+\beta, 0\}& \text{ if } \mathbf{z}_i - \mathbf{x}_{0i} <- \beta. \end{cases}$$

Về cơ bản, nếu thay đổi không lớn hơn ngưỡng $\beta$, chúng ta giữ giá trị ban đầu, còn nếu lớn hơn chúng ta chọn một giá trị gần ảnh gốc nhưng vẫn trong khoảng $(0,1)$ cho đúng domain của ảnh.

Thuật toán đầy đủ của phương pháp EAD như sau:

• Với ảnh đầu vào là $\mathbf{x}$, khởi tạo $\mathbf{x}^{(0)}=\mathbf{y}^{(0)}=\mathbf{x}$
• Với số lần chạy FISTA là $I$, chúng ta update các giá trị trên $I$ lần theo công thức:

$$\mathbf{x}^{(k+1)}=S_\beta(\mathbf{y}^{(k)}-\alpha_k\nabla g(\mathbf{y}^{(k)}))$$

$$\mathbf{y}^{(k+1)}=\mathbf{x}^{(k+1)}+\frac{k}{k+3}(\mathbf{x}^{(k+1)}-\mathbf{x}^{(k)})$$

với $\alpha_k$ là step size cho từng iteration.

• Cuối cùng, check giá trị $\{\mathbf{x}^{(k)}\}_{k=1}^I$ của các iteration xem có cái nào tấn công thành công không.

Phần sử dụng $\mathbf{y}$ chính là cải tiến của FISTA từ thuật toán gốc ISTA.

Kết quả cho thấy tấn công này với $\kappa=0$ có tỉ lệ thành công cao (100%!), ngang ngửa với CW và I-FGM (còn có tên là BIM — đây là phiên bản tiền thân của PGD, click vào link này để biết thêm chi tiết). Trong đó, CW cho khoảng cách $l_2$ bé nhất, I-FGM-$L_\infty$ cho khoảng cách $l_\infty$ bé nhất, và EAD cho khoảng cách $l_1$ bé nhất. Ngoài ra, các adversarial của EAD nhìn có vẻ giống với ảnh gốc nhất.

Còn với $\kappa>0$, độ thành công giảm xuống, tuy nhiên transferability tăng; có nghĩa là adversarial example được sinh ra cho 1 model có thể sử dụng với model khác, bao gồm cả các model được train bằng defensive distillation^[1]. Tuy nhiên, nếu tăng quá cao thì các adversarial example sẽ không còn nằm trong data domain nữa (mà overfit vào model), nên transferability lại giảm xuống.

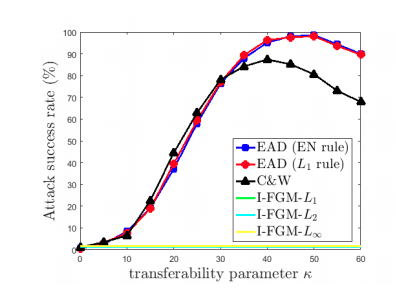
^[1] Defensive distillation là khi sử dụng distillation để dạy cho một mô hình bé hơn bằng adversarial data và soft label của mô hình lớn hơn, dùng để giảm kích cỡ mô hình đồng thời tăng khả năng phòng chống tấn công.

Phần còn lại của paper

Khi $\beta=0$ thì EAD trở thành CW, nên có thể coi EAD là phiên bản mở rộng của CW. Đó cũng là lý do tại sao các adversarial example của EAD có độ khác nhau $l_1$ bé hơn CW, nhưng $l_2$ lớn hơn.

Tác giả không sử dụng Change-of-Variable (phương pháp được sử dụng trong CW để ép adversarial example trong khoảng (0,1)) do không phù hợp với objective $l_1$ trong hàm $f$, vì vậy nên phải sử dụng FISTA thay vì SGD.

Nếu sử dụng tấn công này với adversarial training thì model lại càng tốt.

Bình luận

Tác giả cho rằng MNIST là data khó tấn công nhất do ảnh tập này sửa tí là dễ nhận ra, tuy nhiên cần nhận thấy là dataset này quá đơn giản, khiến cho việc tạo ra adversarial lại rất dễ.

Có thể việc phương pháp này tốt hơn là do thêm các regularization terms khác cho adversarial example nhìn giống ảnh gốc hơn. Vậy nếu chúng ta thêm các norm $l_p$ khác thì sao?

Hết.

Hãy like subscribe và comment vì nó miễn phí?