KNN là gì?

       KNN (K-Nearest Neighbors) là một trong những thuật toán học có giám sát đơn giản nhất được sử dụng nhiều trong khai phá dữ liệu và học máy. Ý tưởng của thuật toán này là nó không học một điều gì từ tập dữ liệu học (nên KNN được xếp vào loại lazy learning), mọi tính toán được thực hiện khi nó cần dự đoán nhãn của dữ liệu mới.
      Lớp (nhãn) của một đối tượng dữ liệu mới có thể dự đoán từ các lớp (nhãn) của k hàng xóm gần nó nhất.

Ví dụ:

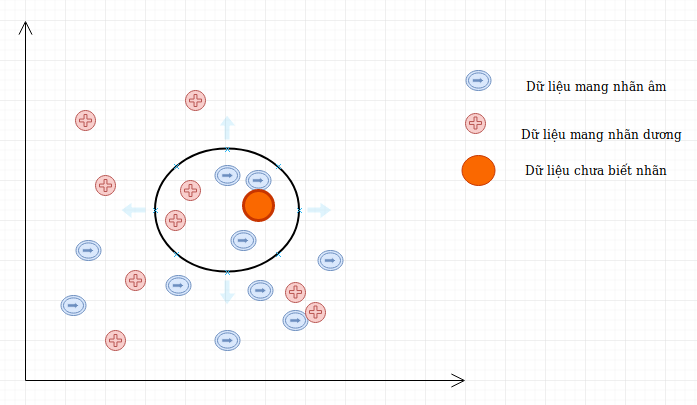
      Giả sử ta có D là tập các dữ liệu đã được phân loại thành 2 nhãn (+) và (-) được biểu diễn trên trục tọa độ như hình vẽ và một điểm dữ liệu mới A chưa biết nhãn. Vậy làm cách nào để chúng ta có thể xác định được nhãn của A là (+) hay (-)?
      Có thể thấy cách đơn giản nhất là so sánh tất cả các đặc điểm của dữ liệu A với tất cả tập dữ liệu học đã được gắn nhãn và xem nó giống cái nào nhất, nếu dữ liệu (đặc điểm) của A giống với dữ liệu của điểm mang nhãn (+) thì điểm A mang nhãn (+), nếu dữ liệu A giống với dữ liệu nhãn (-) hơn thì nó mang nhãn (-), trông có vẻ rất đơn giản nhưng đó là những gì mà KNN làm.
      Trong trường hợp của KNN, thực tế nó không so sánh dữ liệu mới (không được phân lớp) với tất cả các dữ liệu khác, thực tế nó thực hiện một phép tính toán học để đo khoảng cách giữa dữ liệu mới với tất cả các điểm trong tập dữ liệu học D để thực hiện phân lớp. Phép tính khoảng cách giữa 2 điểm có thể là Euclidian, Manhattan, trọng số, Minkowski, …

Các bước trong KNN

1. Ta có D là tập các điểm dữ liệu đã được gắn nhãn và A là dữ liệu chưa được phân loại.
2. Đo khoảng cách (Euclidian, Manhattan, Minkowski, Minkowski hoặc Trọng số) từ dữ liệu mới A đến tất cả các dữ liệu khác đã được phân loại trong D.
3. Chọn K (K là tham số mà bạn định nghĩa) khoảng cách nhỏ nhất.
4. Kiểm tra danh sách các lớp có khoảng cách ngắn nhất và đếm số lượng của mỗi lớp xuất hiện.
5. Lấy đúng lớp (lớp xuất hiện nhiều lần nhất).
6. Lớp của dữ liệu mới là lớp mà bạn đã nhận được ở bước 5.

Ví dụ:

Giả sử ta có tập dữ liệu D có gắn nhãn gồm 15 điểm như trên ảnh.

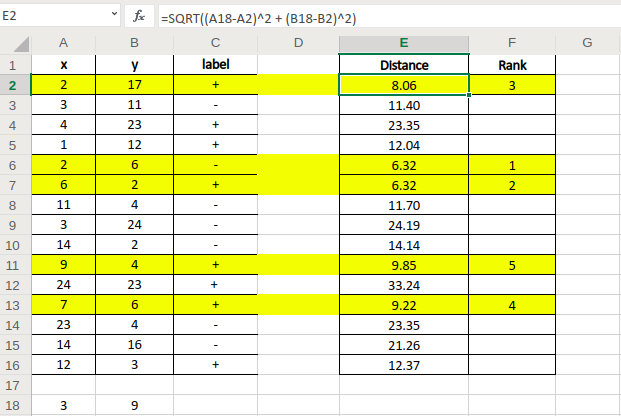
1. Điểm cần dự đoán nhãn A(3,9)
2. Ta tính khoảng cách từ điểm A đến các điểm dữ liệu trong D bằng công thức Euclidian.
3. Ta chọn K= 5, và tìm ra 5 điểm có khoảng cách gần với điểm A nhất.
4. Trong 5 điểm ta thấy có 4 điểm mang nhãn (+) và 1 điểm mang nhãn (-).
5. Vậy ta có thể đưa ra kết luận là điểm A cần dự đoán mang nhãn (+).

Ưu điểm

1. Thuật toán đơn giản, dễ dàng triển khai.
2. Độ phức tạp tính toán nhỏ.
3. Xử lý tốt với tập dữ liệu nhiễu

Nhược điểm

1. Với K nhỏ dễ gặp nhiễu dẫn tới kết quả đưa ra không chính xác
2. Cần nhiều thời gian để thực hiện do phải tính toán khoảng cách với tất cả các đối tượng trong tập dữ liệu.
3. Cần chuyển đổi kiểu dữ liệu thành các yếu tố định tính.

Trong bài tiếp theo chúng ta sẽ xây dựng một mã nguồn mô phỏng thuật toán KNN trong thực tế.